
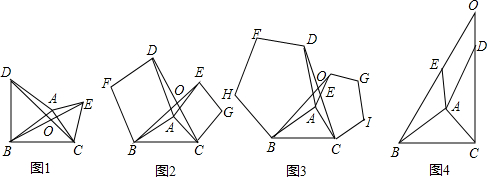
���� ��1���ٸ��ݵȱ�������֤��AB=AD��AC=AE�������õ�ʽ���ʵá�DAC=��BAE������SAS�ó���ABE�ա�ADC���ɣ�
���ȸ��ݡ�ABE�ա�ADC���ó���ABE=��ADC���ٸ��ݡ�BOC�ǡ�BOD����ǣ��õ���BOC=��ODB+��DBA+��ABE���ݴ˽��м��㼴�ɣ�
�����â��з������ó���ABE�ա�ADC���ٸ��ݢ��з�����������á�BOC�Ķ�����
��2������ͼ1�У���BOC=120��=$\frac{360��}{3}$��ͼ2�У���BOC=90��=$\frac{360��}{4}$��ͼ3�У���BOC=72��=$\frac{360��}{5}$���Դ������ҳ����ɣ����ɵó�ͼ4�е�����n����ʱ����BOC=$\frac{360��}{n}$��
���  �⣺��1������ͼ1���ߡ�ABD���ACE��Ϊ�ȱ������Σ�
�⣺��1������ͼ1���ߡ�ABD���ACE��Ϊ�ȱ������Σ�
��AD=AB��AC=AE���ҡ�BAD=��CAE=60�㣬
���BAD+��BAC=��CAE+��BAC��
����DAC=��BAE��
�ڡ�ABE�͡�ADC�У�
$\left\{\begin{array}{l}{AB=AD}\\{��BAE=��DAC}\\{AE=AC}\end{array}\right.$��
���ABE�ա�ADC��SAS����
����ͼ1���ߡ�ABE�ա�ADC��
���ABE=��ADC��
�ߡ�BOC�ǡ�BOD����ǣ�
���BOC=��ODB+��DBA+��ABE
=��ADC+��ODB+��DBA
=��ADB+��DBA
=60��+60��
=120�㣻
����ͼ2�����ı���ABFD���ı���ACGE���������Σ�
��AB=AD��AC=AE����DAB=��EAC=90�㣬
���BAE=��DAC��
ͬ���ɵá�ABE�ա�ADC��
���ABE=��ADC��
�����������ڽǺͿɵã���BOD=��BAD=90�㣬
���BOC=��90�㣻
��ͼ3��ͬ���ɵá�ABE�ա�ADC��
���ABE=��ADC��
�����������ڽǺͿɵã���BOD=��BAD=72�㣬
���BOC=72�㣬
�ʴ�Ϊ��90�㣬72�㣻
��2������ɵã�
ͼ1�У���BOC=120��=$\frac{360��}{3}$��
ͼ2�У���BOC=90��=$\frac{360��}{4}$��
ͼ3�У���BOC=72��=$\frac{360��}{5}$��
�Դ����ƣ�ͼ4�У�������n����ʱ����BOC=$\frac{360��}{n}$��
�ʴ�Ϊ��$\frac{360��}{n}$��
���� ���������������ۺ��⣬��Ҫ������ȫ�������ε��ж������ʡ��ȱ������Ρ����ı��ε�ͼ�ε����ʣ��������Ĺؼ���������n���θ������֤������������ȫ�ȣ���������ȵ�˼�뷽����ͬʱ��Ҫ����������n����ÿһ���ڽǵ��������������ε�һ����ǵ������������ڵ������ڽǺ͵ó����ۣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ�����������ͬ��������ص����������ϣ������ͼ�и�����������Ϣ������������⣺
��ͼ�����������ͬ��������ص����������ϣ������ͼ�и�����������Ϣ������������⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
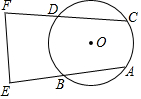 ��ͼ����֪�ڡ�O�У���AB=CD���ӳ�AB��E���ӳ�CD��F��ʹBE=DF����֤��EF�Ĵ�ֱƽ���߾�����O��
��ͼ����֪�ڡ�O�У���AB=CD���ӳ�AB��E���ӳ�CD��F��ʹBE=DF����֤��EF�Ĵ�ֱƽ���߾�����O���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
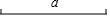 ��1����ͼ����֪�߶�a��������ABC��ʹ��AB=AC��BC=a����AD=$\frac{1}{2}$a��
��1����ͼ����֪�߶�a��������ABC��ʹ��AB=AC��BC=a����AD=$\frac{1}{2}$a���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com