
【题目】如图,抛物线![]() 与
与![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点.
两点.
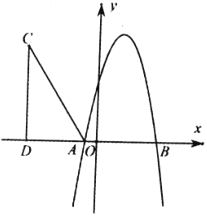
(1)求抛物线的表达式;
(2)在第二象限内取一点![]() ,作
,作![]() 垂直
垂直![]() 轴于点
轴于点![]() ,连结
,连结![]() ,且
,且![]() ,
,![]() .将
.将![]() 沿
沿![]() 轴向右平移
轴向右平移![]() 个单位,当点
个单位,当点![]() 落在抛物线上时,求
落在抛物线上时,求![]() 的值;
的值;
(3)在(2)的条件下,当点![]() 第一次落在抛物线上时记为点
第一次落在抛物线上时记为点![]() ,点
,点![]() 是抛物线对称轴上一点.试探究:在抛物线上是否存在点
是抛物线对称轴上一点.试探究:在抛物线上是否存在点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,若存在,请求出点
为顶点的四边形是平行四边形,若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 的值为7或9;(3)存在,
的值为7或9;(3)存在,![]() 点的坐标为
点的坐标为![]() 或
或![]() 或
或![]()
【解析】
(1)用待定系数法即可求出抛物线的表达式;
(2)先求出点C的坐标,然后根据平移后C点的纵坐标不变,将纵坐标代入抛物线的表达式中求出C平移后的横坐标,根据平移的规律即可得到m的值;
(3)根据第(2)问的结果可知,E点的坐标为(1,8),然后求出抛物线的对称轴,设出P的坐标,然后分两种情况:当![]() 为平行四边形的边时和当
为平行四边形的边时和当![]() 为平行四边形的对角线时,分别进行讨论即可.当
为平行四边形的对角线时,分别进行讨论即可.当![]() 为平行四边形的边时,先证明
为平行四边形的边时,先证明![]() ,则有
,则有![]() ,即可求出Q点横坐标与对称轴之间的距离,从而建立方程求出Q的横坐标,代入抛物线表达式中即可求出纵坐标;当
,即可求出Q点横坐标与对称轴之间的距离,从而建立方程求出Q的横坐标,代入抛物线表达式中即可求出纵坐标;当![]() 为平行四边形的对角线时,利用线段的中点坐标即可求出Q的横坐标,然后代入抛物线表达式中即可求出纵坐标 .
为平行四边形的对角线时,利用线段的中点坐标即可求出Q的横坐标,然后代入抛物线表达式中即可求出纵坐标 .
解:(1)把![]() ,
,![]() 代入
代入![]()
得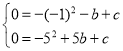 解得
解得![]()
∴抛物线的解表达式是![]() .
.
(2)∵![]() ,且
,且![]() ,
,
∴![]() ,且
,且![]() ,
,
∴![]() .
.
设平移后的点![]() 的对应点为
的对应点为![]() ,则
,则![]() 点的纵坐标为8.
点的纵坐标为8.
代入抛物线解析式可得![]() ,解得
,解得![]() 或
或![]() ,
,
∴![]() 点的坐标为
点的坐标为![]() 或
或![]() .
.
∵![]() ,
,
∴当点![]() 落在抛物线上时,向右平移了7或9个单位.
落在抛物线上时,向右平移了7或9个单位.
∴![]() 的值为7或9.
的值为7或9.
(3)∵![]() ,
,
∴抛物线对称轴为![]() .
.
∴设![]() .
.
由(2)可知![]() 点坐标为
点坐标为![]() .
.
①当![]() 为平行四边形的边时,连接
为平行四边形的边时,连接![]() 交对称轴于点
交对称轴于点![]() ,过
,过![]() 作
作![]() 轴于点
轴于点![]() ,过
,过![]() 作对称轴的垂线,垂足为
作对称轴的垂线,垂足为![]() ,如图,
,如图,
则![]() ,
,
∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
在![]() 和
和![]() 中
中
∴![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,
∴![]() ,解得
,解得![]() 或
或![]() ,
,
当![]() 或
或![]() 时,代入抛物线解析式可求得
时,代入抛物线解析式可求得![]() ,
,
∴![]() 点坐标为
点坐标为![]() 或
或![]() ;
;
②当![]() 为对角线时,
为对角线时,
∵![]() ,
,![]() ,
,
∴线段![]() 的中点坐标为
的中点坐标为![]() ,则线段
,则线段![]() 的中点坐标为
的中点坐标为![]() ,
,
设![]() ,且
,且![]() ,
,
∴![]() ,解得
,解得![]() ,把
,把![]() 代入抛物线解析式可求得
代入抛物线解析式可求得![]() ,
,
∴![]() ;
;
综上可知![]() 点的坐标为
点的坐标为![]() 或
或![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a<0)的图象经过(m+1,a),(m,b)两点.
(1)若m=1,a=-1,求该二次函数的解析式;
(2)求证:am+b=0;
(3)若该二次函数的最大值为![]() ,当x=1时,y≥3a,求a的取值范围.
,当x=1时,y≥3a,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段 AB 经过⊙O 的圆心, AC , BD 分别与⊙O 相切于点 C ,D .若 AC =BD = 4 ,∠A=45°,则弧CD的长度为( )
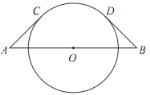
A.πB.2πC.2![]() πD.4π
πD.4π
查看答案和解析>>
科目:初中数学 来源: 题型:
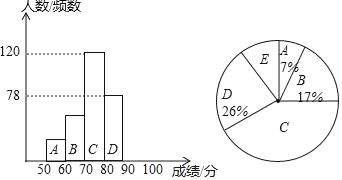
【题目】近日,深圳市人民政府发布了《深圳市可持续发展规划》,提出了要做可持续发展的全球创新城市的目标,某初中学校了解学生的创新意识,组织了全校学生参加创新能力大赛,从中抽取了部分学生成绩,分为5组:A组50~60;B组60~70;C组70~80;D组80~90;E组90~100,统计后得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图.
(1)抽取学生的总人数是 人,扇形C的圆心角是 °;
(2)补全频数直方图;
(3)该校共有2200名学生,若成绩在70分以下(不含70分)的学生创新意识不强,有待进一步培养,则该校创新意识不强的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
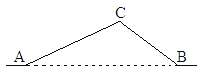
【题目】如图,从A地到B地的公路需要经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°。因城市规划的需要,将在A,B两地之间修建一条笔直的公路。
(1)求改直后的公路AB的长;
(2)问:公路改造后比原来缩短了多少千米?
(sin25°≈0.42,cos25°≈0.91,sin37°≈0.60,tan37°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
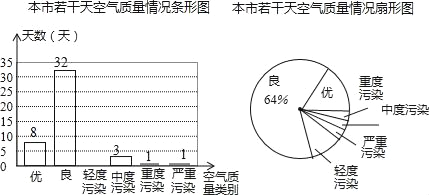
【题目】为了解哈市今年的空气质量情况,环保部门从环境监测网随机抽取了若干天的空气质量情况作为样本进行统计,绘制了如图不完整的统计图:
(1)计算被抽取的天数;
(2)请通过计算补全条形统计图;
(3)请估计哈市这一年(365天)达到优和良的总天数.
查看答案和解析>>
科目:初中数学 来源: 题型:
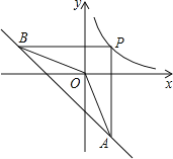
【题目】如图,P为反比例函数y=![]() (k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=-x-6的图象于点A、B.若∠AOB=135°,则k的值是______.
(k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=-x-6的图象于点A、B.若∠AOB=135°,则k的值是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com