
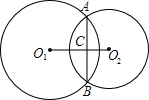
 已知:如图,⊙O1与⊙O2相交于A、B,若两圆半径分别为17cm和10cm,公共弦AB=16cm,求O1O2的长.
已知:如图,⊙O1与⊙O2相交于A、B,若两圆半径分别为17cm和10cm,公共弦AB=16cm,求O1O2的长. 分析 连接O1A、O2A,由相交两圆的性质得出O1O2垂直平分AB,得出∠ACO1=∠ACO2=90°,AC=$\frac{1}{2}$AB=8cm,由勾股定理求出O1C和O2C,O1O2=O1C+O2C,即可得出结果.
解答 解:连接O1 A、O2 A,如图所示: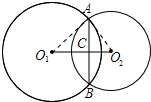
∵⊙O1与⊙O2相交于A、B,
∴O1O2垂直平分AB,
∴∠ACO1=∠ACO2=90°,AC=$\frac{1}{2}$AB=8cm,
由勾股定理得:
O1C=$\sqrt{{O}_{1}{A}^{2}-A{C}^{2}}$=$\sqrt{1{7}^{2}-{8}^{2}}$=15(cm),O2C=$\sqrt{{O}_{2}{A}^{2}-A{C}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6(cm),
∴O1O2=O1 C+O2C=15+6=21(cm).
点评 本题考查了相交两圆的性质、勾股定理;熟练掌握相交两圆的性质,运用勾股定理进行计算是解决问题的关键.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:解答题
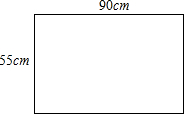 现有一块长为90cm,宽为55cm的木板,能否采用如图的方式,在这块木板上截出两块面积分别是1200平方厘米和2700平方厘米的正方形木板?
现有一块长为90cm,宽为55cm的木板,能否采用如图的方式,在这块木板上截出两块面积分别是1200平方厘米和2700平方厘米的正方形木板?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 20种 | B. | 30种 | C. | 40种 | D. | 50种 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,AC边垂直平分线分别交AB、AC边于D、O两点,作CE∥AB交DO于点E,连接AE、CD.
如图,△ABC中,AC边垂直平分线分别交AB、AC边于D、O两点,作CE∥AB交DO于点E,连接AE、CD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com