
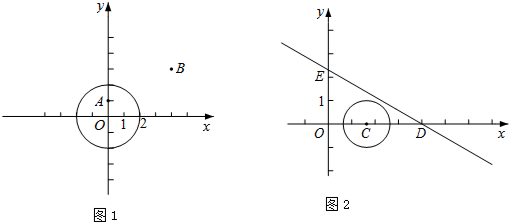
分析 (1)①连接OB,如图1①,只需求出OA、OB就可解决问题;
②设直线l:y=$\frac{3}{4}x+b$与x轴、y轴分别交于点P、Q,过点O作OH⊥PQ于H,设OH与⊙O交于点G,如图1②,可用面积法求出OH,然后根据条件建立关于b的方程,然后解这个方程就可解决问题;
(2)过点C作CN⊥DE于N,如图2.易求出点D、E的坐标,从而可得到OD、OE,然后运用三角函数可求出∠ODE,然后分三种情况(①点C在点D的左边,②点C与点D重合,③点C在点D的右边)讨论,就可解决问题.
解答 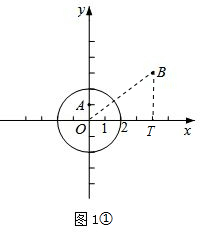 解:(1)①连接OB,过点B作BT⊥x轴于T,如图1①,
解:(1)①连接OB,过点B作BT⊥x轴于T,如图1①,
∵⊙O的半径为2,点A(0,1),
∴d(A,⊙O)=2-1=1.
∵B(4,3),
∴OB=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∴d(B,⊙O)=5-2=3.
故答案为1,3;
②设直线l:y=$\frac{3}{4}x+b$与x轴、y轴分别交于点P、Q,过点O作OH⊥PQ于H,设OH与⊙O交于点G,如图1②,
∴P(-$\frac{4}{3}$b,0),Q(0,b),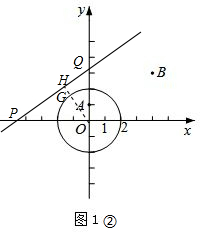 ∴OP=$\frac{4}{3}$|b|,OQ=|b|,
∴OP=$\frac{4}{3}$|b|,OQ=|b|,
∴PQ=$\frac{5}{3}$|b|.
∵S△OPQ=$\frac{1}{2}$OP•OQ=$\frac{1}{2}$PQ•OH,
∴OH=$\frac{OP•OQ}{PQ}$=$\frac{4}{5}$|b|.
∵直线l:y=$\frac{3}{4}x+b$与⊙O的密距d(l,⊙O)=$\frac{6}{5}$,
∴$\frac{4}{5}$|b|=2+$\frac{6}{5}$=$\frac{16}{5}$,
∴b=±4;
(2)过点C作CN⊥DE于N,如图2.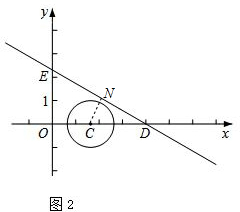 ∵点D、E分别是直线y=-$\frac{\sqrt{3}}{3}x$$+\frac{4\sqrt{3}}{3}$与x轴、y轴的交点,
∵点D、E分别是直线y=-$\frac{\sqrt{3}}{3}x$$+\frac{4\sqrt{3}}{3}$与x轴、y轴的交点,
∴D(4,0),E(0,$\frac{4\sqrt{3}}{3}$),
∴OD=4,OE=$\frac{4\sqrt{3}}{3}$,
∴tan∠ODE=$\frac{OE}{OD}$=$\frac{\sqrt{3}}{3}$,
∴∠ODE=30°.
①当点C在点D左边时,m<4.
∵OC=m,
∴CD=4-m,
∴CN=CD•sin∠CDN=$\frac{1}{2}$(4-m)=2-$\frac{1}{2}$m.
∵线段DE与⊙C的密距d(DE,⊙C)<$\frac{1}{2}$,
∴0<2-$\frac{1}{2}$m<$\frac{1}{2}$+1,
∴1<m<4;
②当点C与点D重合时,m=4.
此时d(DE,⊙C)=0.
③当点C在点D的右边时,m>4.
∵线段DE与⊙C的密距d(DE,⊙C)<$\frac{1}{2}$,
∴CD<$\frac{1}{2}$,
∴m-4<$\frac{1}{2}$+1,
∴m<$\frac{11}{2}$
∴4<m<$\frac{11}{2}$.
综上所述:1<m<$\frac{11}{2}$.
点评 本题属于新定义型,主要考查了直线上点的坐标特征、勾股定理、三角函数、三角形的面积公式等知识,运用分类讨论是解决第(2)小题的关键,特别需要注意的是不要把“线段DE与⊙C的密距”与“直线DE与⊙C的密距”相混淆.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:填空题
 如图,已知A1(1,0),A2(1,-1),A3(-1,-1),A4(-1,1),A5(2,1),…则点A2016的坐标是(-504,504).
如图,已知A1(1,0),A2(1,-1),A3(-1,-1),A4(-1,1),A5(2,1),…则点A2016的坐标是(-504,504).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
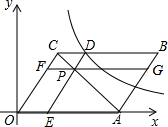 如图,平面直角坐标系中,平行四边形OABC的顶点C(3,4),边OA落在x正半轴上,P为线段AC上一点,过点P分别作DE∥OC,FG∥OA交平行四边形各边如图.若反比例函数$y=\frac{k}{x}$的图象经过点D,四边形BCFG的面积为8,则k的值为( )
如图,平面直角坐标系中,平行四边形OABC的顶点C(3,4),边OA落在x正半轴上,P为线段AC上一点,过点P分别作DE∥OC,FG∥OA交平行四边形各边如图.若反比例函数$y=\frac{k}{x}$的图象经过点D,四边形BCFG的面积为8,则k的值为( )| A. | 16 | B. | 20 | C. | 24 | D. | 28 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
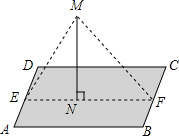 “五一期间”某公司在一块平行四边形ABCD的湖中,立有一个旗杆MN,MN与湖面垂直,旗杆顶端M与湖岸的E、F两处用绳子相连.绳子上系满了彩旗.且直线EF经过旗杆底部N,EF∥AB,已知,AB=40($\sqrt{3}$+1)m.BC=30m.∠MEN=60°,∠MFN=45°,求绳子EM的长.
“五一期间”某公司在一块平行四边形ABCD的湖中,立有一个旗杆MN,MN与湖面垂直,旗杆顶端M与湖岸的E、F两处用绳子相连.绳子上系满了彩旗.且直线EF经过旗杆底部N,EF∥AB,已知,AB=40($\sqrt{3}$+1)m.BC=30m.∠MEN=60°,∠MFN=45°,求绳子EM的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com