
【题目】在菱形ABCD中,∠ABC=60°,延长BA至点F,延长CB至点E,使BE=AF,连结CF,EA,AC,延长EA交CF于点G.
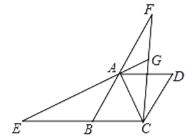
(1)求证:△ACE≌△CBF;
(2)求∠CGE的度数.
【答案】(1)见解析;(2)60°
【解析】
(1)由题意△ABC是等边三角形,可得BC=AC,∠ACB=∠ABC,再求出CE=BF,然后利用“边角边”证明即可;
(2)由(1)△ACE≌△CBF,可得∠E=∠F,然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠CGE=∠ABC即可.
(1)证明:∵AB=AC,∠ABC=60°,
∴△ABC是等边三角形,
∴BC=AC,∠ACB=∠ABC,
∵BE=AF,
∴BE+BC=AF+AB,
即CE=BF,
在△ACE和△CBF中,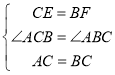 ,
,
∴△ACE≌△CBF(SAS);
(2)解:由(1)可知:△ABC是等边三角形,△ACE≌△CBF,
∴∠E=∠F,
∵∠BAE=∠FAG,
∴∠E+∠BAE=∠F+∠FAG,
∴∠CGE=∠ABC,
∵∠ABC=60°,
∴∠CGE=60°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将![]() 绕点
绕点![]() 顺时针旋转到
顺时针旋转到![]() 的位置,点
的位置,点![]() 、
、![]() 分别落在点
分别落在点![]() 、
、![]() 处,点
处,点![]() 在
在![]() 轴上,再将
轴上,再将![]() 绕点
绕点![]() 顺时针旋转到
顺时针旋转到![]() 的位置,点
的位置,点![]() 在
在![]() 轴上,将
轴上,将![]() 绕点
绕点![]() 顺时针旋转到
顺时针旋转到![]() 的位置,点
的位置,点![]() 在
在![]() 轴上,依次进行下去……,若点
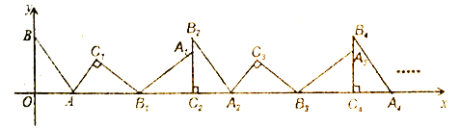
轴上,依次进行下去……,若点![]() ,
,![]() .则点
.则点![]() 的坐标是( )
的坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆市旅游文化商店自制了一款文化衫,每件成本价为20元,每天销售150件:
(1)若要每天的利润不低于2250元,则销售单价至少为多少元?
(2)为了回馈广大游客,同时也为了提高这种文化衫的认知度,商店决定在“五一”节当天开展促销活动,若销售单价在(1)中的最低销售价的基础上再降低![]() m%,则日销售量可以在150件基础上增加
m%,则日销售量可以在150件基础上增加![]() m件,结果当天的销售额达到5670元;要使销售量尽可能大,求出m的值.
m件,结果当天的销售额达到5670元;要使销售量尽可能大,求出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是等腰直角三角形,∠A=90°,点D是腰AC上的一个动点,过C作CE垂直于BD的延长线,垂足为E.
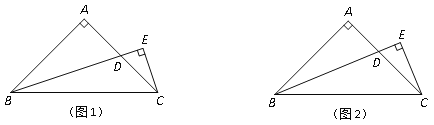
(1)若BD是AC边上的中线,如图1,求![]() 的值;
的值;
(2)若BD是∠ABC的角平分线,如图2,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个测量弹跳力的体育器材,如图所示,竖杆![]() 的长度分别为200厘米和300厘米,
的长度分别为200厘米和300厘米,![]() 厘米.现有一人站在斜杆
厘米.现有一人站在斜杆![]() 下方的点
下方的点![]() 处,直立、单手上举时中指指尖(点
处,直立、单手上举时中指指尖(点![]() )到地面的高度
)到地面的高度![]() 厘米,屈膝尽力跳起时,中指指尖刚好触到斜杆的点
厘米,屈膝尽力跳起时,中指指尖刚好触到斜杆的点![]() 处,此时,就将
处,此时,就将![]() 与
与![]() 的差值
的差值![]() (厘米)作为此人此次的弹跳成绩,设
(厘米)作为此人此次的弹跳成绩,设![]() 厘米.
厘米.
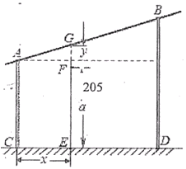
(1)用含![]() 的代数式表示
的代数式表示![]() ;
;
(2)若他弹跳时的位置为![]() ,求该人的弹跳成绩.
,求该人的弹跳成绩.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 是等边三角形,D 为 CB 延长线上一点,E 为 BC 延长线上点.
(1)当 BD、BC 和 CE 满足什么条件时,△ADB∽△EAC?
(2)当△ADB∽△EAC 时,求∠DAE 的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习完北师大教材九年级上册第四章第6节“利用相似三角形测高”后,数学兴趣小组的3名同学利用课余时间想要测量学校里两棵树的高度.在同一时刻的阳光下,他们合作完成了以下工作:
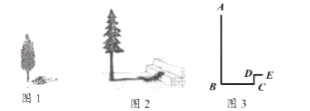
①测得一根长为l米的竹竿的影长为0.8米,甲树的影长为4.08米(如图l).
②测量的乙树的影子除落在地面上外,还有一部分落在教学楼的第一级台阶上(如图2),测得落在地面上的影长为4.4米,一级台阶高为0.3米,落在第一级台阶的影子长为0.2米.
(1)在横线上直接填写甲树的高度为_____________米.
(2)图3为图2的示意图,请利用图3求出乙树的高度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com