
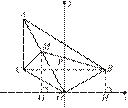
如图1,已知线段AC∥y轴,点B在第一象限,且AO平分∠BAC,AB交y轴与G,连OB、OC.
(1)判断△AOG的形状,并予以证明;
(2)若点B、C关于y轴对称,求证:AO⊥BO;
(3)在(2)的条件下,如图2,点M为OA上一点,且∠ACM=45°,BM交y轴于P,若点B的坐标为(3,1),求点M的坐标.

 解:(1)等腰三角形,证明略.
解:(1)等腰三角形,证明略.
(2)解法一:设BC交y轴于K,过A作AN⊥y轴于N,
易证AN=CK=BK,△ANG≌△BKG,∴AG=BG,
又易证AG=OG,故设∠OAG=∠AOG=x,
∠GOB=∠GBO=y,∴2x+2y=180°,x+y=90°,
∴AO⊥BO.
 解法二:连BC,∵B、C关于y轴对称,AC//y轴,∴AC⊥BC,
解法二:连BC,∵B、C关于y轴对称,AC//y轴,∴AC⊥BC,
易证△COD≌△BOE(HL),∴∠DCO=∠ABO,
∴∠BAC+∠BOC=180° ,设∠BAO=∠CAO=x,
∠OBC=∠OCB=y,∴2x+∠BOC=180° ,
又2y+∠BOC=180° ,∴x=y,故∠OAC=∠OBC,
∴∠AOB=∠ACB=90°,∴AO⊥OB. …… ……7′
(3)连BC,则∠ACB=90°,∵∠ACM=45° ,∴CM平分∠ACB,又AM平分∠BAC,∴BM平分∠ABC,设∠ABM=∠CBM=z,由(2)可得∠OMB=x+z, ∠OBM=y+z=x+z ∴∠OMB=∠OBM,∴OM=OB 故△OBM为等腰直角△,作MG⊥x轴于G,BH⊥x轴于H,易证△OMG≌△OBH,∴OG=BH=1,MG=OH=3∴M(-1,3).…


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:
在△ABC与△DEF中,已知BC=EF;∠C=∠F;再加一个条件,却不能判断△ABC与△DEF全等的是 ( ).
A. AB=DE B.AC=DF C.∠B=∠E D.∠A=∠D

查看答案和解析>>
科目:初中数学 来源: 题型:
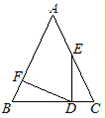
如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB,垂足为E,且AB=6cm,则△DEB的周长为( )
A. 4cm B. 6cm C. 8cm D. 10cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com