
【题目】某城市为了加强公民的节气和用气意识,按以下规定收取每月煤气费:所用煤气如果不超过50立方米,按每立方米0.8元收费;如果超过50立方米,超过部分按每立方米1.2元收费设小丽家每月所用煤气量为x立方米,应交煤气费为y元.
(1)若小丽家某月所用煤气量为80立方米,则小丽家该月应交煤气费多少元?
(2)试写出y与x之间的解析式.
(3)若小丽家4月份的煤气费为88元,则她家4月份所用煤气量为多少立方米?
(4)已知小丽家6月份所交的煤气费平均每立方米为0.95元,那么6月份小丽家用了多少立方米的煤气?
【答案】(1)76元;(2)![]() ;(3)小丽家4月份所用煤气量为90立方米;(4)6月份小丽家用了80立方米的煤气.
;(3)小丽家4月份所用煤气量为90立方米;(4)6月份小丽家用了80立方米的煤气.
【解析】
(1)根据题意计算即可;
(2)根据自变量的取值范围分类讨论,分别求出对应的关系式即可;
(3)设小丽家4月份所用煤气量为a立方米,先判断a是否大于50,然后代入对应的关系式中求值即可;
(4)设6月份小丽家用了b立方米的煤气,先判断b是否大于50,然后根据题意列方程,并解方程即可;
解:(1)根据题意得小丽家该月应交煤气费![]() (元)
(元)
答:小丽家该月应交煤气费76元.
(2)当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
所以y与x之间的解析式为![]() .
.
(3)设小丽家4月份所用煤气量为a立方米.
因为![]() (元),而88元>40元,
(元),而88元>40元,
所以小丽家4月份所用煤气量超过50立方米.
根据题意得![]() ,解得
,解得![]() .
.
答:小丽家4月份所用煤气量为90立方米.
(4)设6月份小丽家用了b立方米的煤气.
∵0.8<0.95
∴小丽家6月份所用煤气量超过50立方米
根据题意得![]() ,
,
解得![]() .
.
答:6月份小丽家用了80立方米的煤气.


 每课必练系列答案
每课必练系列答案科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,O是坐标原点,长方形OACB的顶点A、B分别在x轴与y轴上,已知OA=6,OB=10.点D为y轴上一点,其坐标为(0,2),点P从点A出发以每秒2个单位的速度沿线段AC﹣CB的方向运动,当点P与点B重合时停止运动,运动时间为t秒.
(1)当点P经过点C时,求直线DP的函数解析式;
(2)①求△OPD的面积S关于t的函数解析式;
②如图②,把长方形沿着OP折叠,点B的对应点B′恰好落在AC边上,求点P的坐标.
(3)点P在运动过程中是否存在使△BDP为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于一次函数y=﹣2x+3,下列结论正确的是( )
A. 图象过点(1,﹣1) B. 图象经过一、二、三象限
C. y随x的增大而增大 D. 当x>![]() 时,y<0
时,y<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为选拔一名选手参加“美丽邵阳,我为家乡做代言”主题演讲比赛,经研究,按图所示的项目和权数对选拔赛参赛选手进行考评(因排版原因统计图不完整).下表是李明、张华在选拔赛中的得分情况:
项目 选手 | 服装 | 普通话 | 主题 | 演讲技巧 |
李明 | 85 | 70 | 80 | 85 |
张华 | 90 | 75 | 75 | 80 |
结合以上信息,回答下列问题:
(1)求服装项目的权数及普通话项目对应扇形的圆心角大小;
(2)求李明在选拔赛中四个项目所得分数的众数和中位数;
(3)根据你所学的知识,帮助学校在李明、张华两人中选择一人参加“美丽邵阳,我为家乡做代言”主题演讲比赛,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 边上.
边上.
(1)如图1,连接![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长度;
的长度;
(2)如图2,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,旋转过程中,直线
,旋转过程中,直线![]() 分别与直线
分别与直线![]() 交于点
交于点![]() ,当
,当![]() 是等腰三角形时,直接写出
是等腰三角形时,直接写出![]() 的值;
的值;
(3)如图3,将![]() 绕点
绕点![]() 顺时针旋转,使得点
顺时针旋转,使得点![]() 在同一条直线上,点
在同一条直线上,点![]() 为
为![]() 的中点,连接
的中点,连接![]() .猜想
.猜想![]() 和
和![]() 之间的数量关系并证明.
之间的数量关系并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
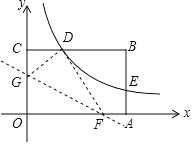
【题目】如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为BC边上的点,AB=BD,反比例函数![]() 在第一象限内的图象经过点D(m,2)和AB边上的点E(n,
在第一象限内的图象经过点D(m,2)和AB边上的点E(n,![]() ).
).
(1)求m、n的值和反比例函数的表达式.
(2)将矩形OABC的一角折叠,使点O与点D重合,折痕分别与x轴,y轴正半轴交于点F,G,求线段FG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com