
【题目】一只蚂蚁从![]() 点出发,在一条直线上来回爬行,把它向右爬行的路程记为正数,向左爬行的路程记为负数,则它爬过的各段路程依次为
点出发,在一条直线上来回爬行,把它向右爬行的路程记为正数,向左爬行的路程记为负数,则它爬过的各段路程依次为
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
(1)蚂蚁离出发点最远时是多少厘米?是在出发点的左边还是右边?
(2)蚂蚁在爬行过程中,如果每爬行![]() 就得到1粒瓜子,那么最后它共得到多少粒瓜子?
就得到1粒瓜子,那么最后它共得到多少粒瓜子?
【答案】(1)蚂蚁在爬行过程中离出发点M最远时是10厘米;在出发点的右边;(2)在爬行过程中,最后它共得到27粒瓜子.
【解析】
(1)分别计算出每次爬行后的位置;
(2)蚂蚁一共得到的瓜子数,与它爬行的方向无关,只与爬行的距离有关,所以应把绝对值相加,再求得到的瓜子数.
解:(1)3+10=7(cm),78=1(cm),1+5=4(cm),46=2(cm),2+12=10(cm),1010=0(cm),
∴蚂蚁在爬行过程中离出发点M最远时是10厘米;在出发点的右边;
(2)蚂蚁从离开出发点开始走的路程是:
|3|+|+10|+|8|+|+5|+|6|+|12|+|10|=54(厘米),
在爬行过程中,蚂蚁得到的瓜子数是:54÷2=27(粒)
答:在爬行过程中,最后它共得到27粒瓜子.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】选择适当的方法解下列方程:
(1)3(x+1)2=27; (2)2x2+6=7x;
(3)3x(x-2)=2(2-x); (4)y2-4y-3=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于只有1张市运动会开幕式的门票,小王和小张都想去,两人商量采取转转盘(如图,转盘盘面被分为面积相等,且标有数字1,2,3,4的4个扇形区域)的游戏方式决定谁胜谁去观看.规则如下:两人各转动转盘一次,当转盘指针停止,如两次指针对应盘面数字都是奇数,则小王胜;如两次指针对应盘面数字都是偶数,则小张胜;如两次指针对应盘面数字是一奇一偶,视为平局.若为平局,继续上述游戏,直至分出胜负.
如果小王和小张按上述规则各转动转盘一次,则
(1)小王转动转盘,当转盘指针停止,对应盘面数字为奇数的概率是多少?
(2)该游戏是否公平?请用列表或画树状图的方法说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列短文,并回答下列问题:我们把相似的概念推广到空间:如果两个几何体大小不一定相等,但形状完全相同,我们就把它们叫作相似体.
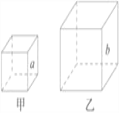
如图,甲、乙是两个不同的正方体,正方体都是相似体,它们的一切对应线段之比都等于相似比( a ∶ b ),设S 甲 ,S 乙 分别表示这两个正方体的表面积,则![]()
.又设V 甲 ,V 乙 分别表示这两个正方体的体积,则![]() .
.
(1)下列几何体中,一定属于相似体的是(___)
A.两个球体 B.两个圆锥体
C.两个圆柱体 D.两个长方体
(2)请归纳出相似体的三个主要性质:①相似体的一切对应线段(或弧)的比等于__________;②相似体的表面积的比等于__________;③相似体的体积比等于__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC、BD交于点O,DE平分∠ADC交AB于点E,∠BCD=60°,AD=![]() AB,连接OE.下列结论:①SABCD=ADBD;②DB平分∠CDE;③AO=DE;④S△ADE=5S△OFE,其中正确的个数有( )
AB,连接OE.下列结论:①SABCD=ADBD;②DB平分∠CDE;③AO=DE;④S△ADE=5S△OFE,其中正确的个数有( )
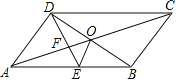
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
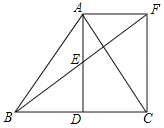
【题目】如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=CD,连接CF.
(1)求证:△AEF≌△DEB;
(2)若AB=AC,试判断四边形ADCF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节当天,小明带了四个粽子(除味道不同外,其它均相同),其中两个是大枣味的,另外两个是火腿味的,准备按数量平均分给小红和小刚两个好朋友.
(1)请你用树状图或列表的方法表示小红拿到的两个粽子的所有可能性;
(2)请你计算小红拿到的两个粽子刚好是同一味道的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com