
 如图,Rt△ABC∽Rt△ADE,∠BCA=30°,F,M,N分别为BE,BC,DE的中点.①△BDA∽△CEA;②BD⊥CE;③∠MFN=90°;④MF=2NF.上述结论中正确的个数有( )
如图,Rt△ABC∽Rt△ADE,∠BCA=30°,F,M,N分别为BE,BC,DE的中点.①△BDA∽△CEA;②BD⊥CE;③∠MFN=90°;④MF=2NF.上述结论中正确的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据相似三角形的性质得到∠AED=∠BCA=30°,根据三角函数的定义得到$\frac{AB}{AC}=\frac{AD}{AE}$=$\frac{\sqrt{3}}{3}$,于是推出△BDA∽△CEA;故①正确;由相似三角形的性质得到∠DBA=∠ACE,由三角形的内角和得到∠CGH=∠BAH=90°,于是得到BD⊥CE,故②正确;根据三角形的中位线即可得到∠MFN=90°,故③正确;由三角形的中位线的性质得到NF=$\frac{1}{2}$BD,MF=$\frac{1}{2}$CE,根据相似三角形的性质得到$\frac{BD}{CE}$=$\frac{AB}{AC}$=$\frac{\sqrt{3}}{3}$,等量代换得到$\frac{NF}{FM}$=$\frac{\sqrt{3}}{3}$,故④错误.
解答 解:∵Rt△ABC∽Rt△ADE,
∴∠AED=∠BCA=30°,
∴$\frac{AB}{AC}=\frac{AD}{AE}$=$\frac{\sqrt{3}}{3}$,
∵∠BAC=∠DAE=90°,
∴∠BAD=∠EAC,
∴△BDA∽△CEA;故①正确;
∴∠DBA=∠ACE,
∵ ∠BHA=∠CHG,
∠BHA=∠CHG,
∴∠CGH=∠BAH=90°,
∴BD⊥CE,故②正确;
∵F,M,N分别为BE,BC,DE的中点,
∴MF∥CE,NF∥BG,
∴MF⊥BD,
∴MF⊥NF,
∴∠MFN=90°,故③正确;
∵NF=$\frac{1}{2}$BD,MF=$\frac{1}{2}$CE,
∵△BDA∽△CEA,
∴$\frac{BD}{CE}$=$\frac{AB}{AC}$=$\frac{\sqrt{3}}{3}$,
∴$\frac{NF}{FM}$=$\frac{\sqrt{3}}{3}$,故④错误,
∴正确的结论有3个,
故选C.
点评 本题考查了相似三角形的判定和性质,三角形的内角和,三角形的中位线的性质,平行线的判定和性质,熟练掌握各定理是解题的关键.


科目:初中数学 来源: 题型:解答题
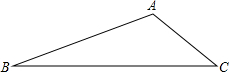 如图,在△ABC中,∠BAC是钝角,按要求完成下列画图.(不写作法,保留作图痕迹,并分别写出结论)
如图,在△ABC中,∠BAC是钝角,按要求完成下列画图.(不写作法,保留作图痕迹,并分别写出结论)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
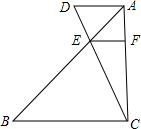 如图,线段AB、CD相交于点E,AD∥EF∥BC.若AE:EB=1:2,S△ADE=1,则AF:AC=$\frac{1}{3}$,S△AEF=$\frac{2}{3}$.
如图,线段AB、CD相交于点E,AD∥EF∥BC.若AE:EB=1:2,S△ADE=1,则AF:AC=$\frac{1}{3}$,S△AEF=$\frac{2}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3,4,5 | B. | 5,12,13 | C. | 12,15,25 | D. | 0.7,2.4,2.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com