
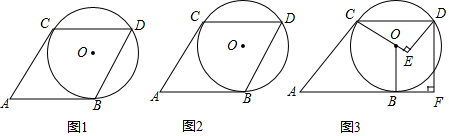
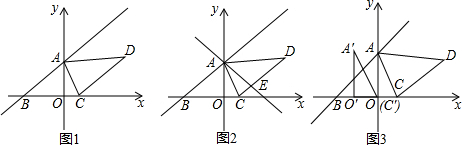
分析 (1)如图1,连接OC,OB,利用切线的性质和四边形内角和是360°解答;
(2)如图2,连接AO,OB,求得OB的长度即可;
(3)作GH⊥OB于H,则HG=BF,设BF=HG=x,得到CE=$\sqrt{3}$x,连接OD,解直角三角形即可得到结论.
解答 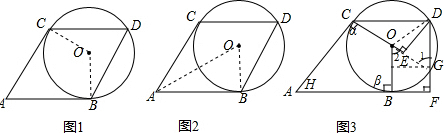 解:(1)如图1,连接OC,OB,
解:(1)如图1,连接OC,OB,
∵AB、AC为⊙O的切线,
∴∠ACO=∠ABO=90°,
∴∠O=180°-∠A,
∵∠O=2∠D,
∴∠A+2∠D=180°;
(2)如图2,连接AO,OB,
∵AB是⊙O的切线,
∴∠ABO=90°,∠OAB=$\frac{1}{2}∠$CAB,
∵∠D=60°,
∴∠CAB=180°-2∠D=60°,
∴∠OAB=30°,
∵AB=6$\sqrt{3}$,
∴OB=6,
∴⊙O的半径是6;
(3)∵∠α=∠β=90°,
∵∠A=60°,
∴∠2=60°,
∵DF⊥AB,OB⊥AB,
∴OB∥FD,
∴∠1=∠2=60°,
作GH⊥OB于H,则HG=BF,设BF=HG=x,
∵CE=$\sqrt{3}$BF,
∴CE=$\sqrt{3}$x,
连接OD,由(2)知,OB=OC=OD=6,
∴OE=CE-OC=$\sqrt{3}$x-6,
∵DE⊥CE,
∴在Rt△ODE中,DE=$\sqrt{O{D}^{2}-O{E}^{2}}$=$\sqrt{12\sqrt{3}x-3{x}^{2}}$,
在Rt△DEG中,tan∠1=$\frac{DE}{EG}$=tan60°=$\sqrt{3}$,
∴EG=$\frac{DE}{\sqrt{3}}$=$\sqrt{4\sqrt{3}x-{x}^{2}}$,
∴OG=OE+EG=$\sqrt{3}$x-6+$\sqrt{4\sqrt{3}x-{x}^{2}}$,
∵HG⊥OB,
∴在Rt△OHG中,sin∠2=$\frac{HG}{OG}$=sin60°=$\frac{\sqrt{3}}{2}$,
∵HG=x,
∴2HG=$\sqrt{3}$OG,
∴2x=$\sqrt{3}$($\sqrt{3}$x-6+$\sqrt{4\sqrt{3}x-{x}^{2}}$),
∴6$\sqrt{3}$-x=$\sqrt{12\sqrt{3}x-3{x}^{2}}$,
解得:x=3$\sqrt{3}$,
∴BF=3$\sqrt{3}$,
∴CE=9,DE=$\sqrt{27}$=3$\sqrt{3}$,
∴CD=$\sqrt{C{E}^{2}+D{E}^{2}}$=6$\sqrt{3}$.
点评 本题考查了切线的性质,解直角三角形,熟练掌握解直角三角形的方法是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
 如图,把一张对面互相平行的纸条折成如图那样,EF是折痕,若∠EFB=34°,则下列结论正确有4个
如图,把一张对面互相平行的纸条折成如图那样,EF是折痕,若∠EFB=34°,则下列结论正确有4个查看答案和解析>>
科目:初中数学 来源: 题型:选择题
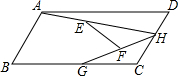 如图,在平行四边形ABCD中,∠C=120°,AD=2AB=4,点H、G分别是边AD、BC上的动点.连接AH、HG,点E为AH的中点,点F为GH的中点,连接EF.则EF的最大值与最小值的差为( )
如图,在平行四边形ABCD中,∠C=120°,AD=2AB=4,点H、G分别是边AD、BC上的动点.连接AH、HG,点E为AH的中点,点F为GH的中点,连接EF.则EF的最大值与最小值的差为( )| A. | 1 | B. | $\sqrt{3}$-1 | C. | $\frac{\sqrt{3}}{2}$ | D. | 2-$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 笔试成绩 | 66 | 90 | 86 | 64 | 66 | 84 |
| 专业技能测试成绩 | 95 | 92 | 93 | 80 | 88 | 92 |
| 说课成绩 | 85 | 78 | 86 | 88 | 94 | 85 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com