
【题目】如图①,一次函数y=kx+b的图象与二次函数y=x2的图象相交于A,B两点,点A,B的横坐标分别为m,n(m<0,n>0).
(1)当m=﹣1,n=4时,k= ,b= ;
当m=﹣2,n=3时,k= ,b= ;
(2)根据(1)中的结果,用含m,n的代数式分别表示k与b,并证明你的结论;
(3)利用(2)中的结论,解答下列问题:
如图②,直线AB与x轴,y轴分别交于点C,D,点A关于y轴的对称点为点E,连接AO,OE,ED.
①当m=﹣3,n>3时,求 ![]() 的值(用含n的代数式表示);
的值(用含n的代数式表示);
②当四边形AOED为菱形时,m与n满足的关系式为_____ ;
当四边形AOED为正方形时,m= , n= .
【答案】
(1)
解:当x=﹣1时,y=x2=1,则A(﹣1,1);当x=4时,y=x2=16,则B(4,16),
把A(﹣1,1)、B(4,16)分别代入y=kx+b得![]() ,解得
,解得![]() ;
;
当x=﹣2时,y=x2=4,则A(﹣2,4);当x=3时,y=x2=9,则B(3,9),
把A(﹣2,4)、B(3,9)分别代入y=kx+b得![]() ,解得
,解得![]() ;
;
故答案为:3,4;1,6;
(2)
解:k=m+n,b=﹣mn.理由如下:
把A(m,m2),B(n,n2)代入y=kx+b得![]() ,解得
,解得![]() ;
;
(3)
解:①当m=﹣3时,A(﹣3,9),
∵点A关于y轴的对称点为点E,
∴E(3,9),
∵k=m+n,b=﹣mn,
∴k=﹣3+n,b=3n,
∴直线AB的解析式为y=(﹣3+n)x+3n,则D(0,3n),
当y=0时,(﹣3+n)x+3n=0,解得x=![]() ,则C(
,则C(![]() ,0),
,0),
∴![]() =
=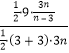 =
=![]() (n>3);
(n>3);
②连结AE交OD于P,如图②,
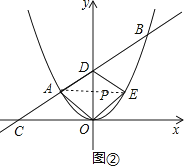
∵点A(m,m2)关于y轴的对称点为点E,
∴E(﹣m,m2),
∴OP=m2,
∵k=m+n,b=﹣mn,
∴D(0,﹣mn),
若四边形AOED为菱形,则OP=DP,即﹣mn=2m2,所以n=﹣2m;
若四边形AOED为正方形,则OP=AP,即﹣m=m2,解得m=﹣1,所以n=﹣2m=2.
【解析】(1)根据二次函数图象上点的坐标特征,由当m=﹣1,n=4得A(﹣1,1),B(4,16),然后利用待定系数法求出直线AB的解析式即可得到k和b的值;当m=﹣2,n=3时,用同样的方法求解;
(2)根据二次函数图象上点的坐标特征得到A(m,m2),B(n,n2),把它们分别代入y=kx+b得![]() ,然后解关于k、b的方程组即可得到k=m+n,b=﹣mn;
,然后解关于k、b的方程组即可得到k=m+n,b=﹣mn;
(3)①当m=﹣3时,A(﹣3,9),根据y轴对称的点的坐标特征得E(3,9),再由(2)的结论得k=m+n,b=﹣mn,则直线AB的解析式为y=(﹣3+n)x+3n,接着求出D(0,3n),C(![]() ,0),然后根据三角形面积公式可计算出
,0),然后根据三角形面积公式可计算出 ![]() 的值;
的值;
②连结AE交OD于P,如图②,点A(m,m2)关于y轴的对称点E的坐标为(﹣m,m2),则OP=m2 , 由于k=m+n,b=﹣mn,则D(0,﹣mn);若四边形AOED为菱形,根据菱形的性质OP=DP,即﹣mn=2m2 , 可解得n=﹣2m;若四边形AOED为正方形,根据正方形的性质得OP=AP=OP=PD,易得m=﹣1,n=2.


科目:初中数学 来源: 题型:
【题目】如图,有一矩形纸片ABCD,AB=6,AD=8,将纸片折叠使AB落在AD边上,折痕为AE,再将△ABE以BE为折痕向右折叠,AE与CD交于点F,则 ![]() 的值是( )
的值是( ) 
A.1
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,点E,F分别在AB,CD上,连接EF,∠AEF、∠CFE的平分线交于点G,∠BEF、∠DFE的平分线交于点H.
(1)求证:四边形EGFH是矩形
(2)小明在完成(1)的证明后继续进行了探索,过G作MN∥EF,分别交AB,CD于点M,N,过H作PQ∥EF,分别交AB,CD于点P,Q,得到四边形MNQP,此时,他猜想四边形MNQP是菱形,请在下列框中补全他的证明思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为8cm,E、F、G、H分别是AB、BC、CD、DA上的动点,且AE=BF=CG=DH.
(1)求证:四边形EFGH是正方形
(2)判断直线EG是否经过一个定点,并说明理由
(3)求四边形EFGH面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的北偏东53°方向,距离灯塔100海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处.
(参考数据:sin53°=0.80,cos53°=0.60,tan53°=0.33,![]() =1.41)
=1.41)
(1)在图中画出点B,并求出B处与灯塔P的距离(结果取整数);
(2)用方向和距离描述灯塔P相对于B处的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,已知AD>AB.在边AD上取点E,使AE=AB,连结CE,过点E作EF⊥CE,与边AB或其延长线交于点F.
猜想:如图①,当点F在边AB上时,线段AF与DE的大小关系为______.
探究:如图②,当点F在边AB的延长线上时,EF与边BC交于点G.判断线段AF与DE的大小关系,并加以证明.
应用:如图②,若AB=2,AD=5,利用探究得到的结论,求线段BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大学生小刘回乡创办小微企业,初期购得原材料若干吨,每天生产相同件数的某种产品,单件产品所耗费的原材料相同.当生产6天后剩余原材料36吨,当生产10天后剩余原材料30吨.若剩余原材料数量小于或等于3吨,则需补充原材料以保证正常生产.
(1)求初期购得的原材料吨数与每天所耗费的原材料吨数;
(2)若生产16天后,根据市场需求每天产量提高20%,则最多再生产多少天后必须补充原材料?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com