
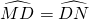 ,EH-HF=2.设∠ACB=a,ta
,EH-HF=2.设∠ACB=a,ta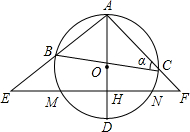 na=
na= ,EH和HF是方程x2-(k+2)x+4k=0的两个实数根.
,EH和HF是方程x2-(k+2)x+4k=0的两个实数根.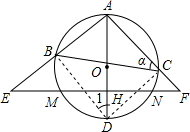 解:(1)依题意,及一元二次方程根与系数关系,得
解:(1)依题意,及一元二次方程根与系数关系,得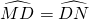 ,
, =tana=
=tana= ,又EH=8,
,又EH=8,
 =tana=
=tana= ,
, AD
AD AH=
AH= ×6=8
×6=8 ,
, ,
,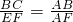
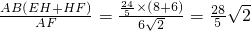 ;
; ,
,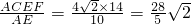 .
. ,结合EH=8,可求AH,再利用勾股定理可求AE,在Rt△AHF中,利用勾股定理可求AF,在Rt△ABD中,由于tan∠1=
,结合EH=8,可求AH,再利用勾股定理可求AE,在Rt△AHF中,利用勾股定理可求AF,在Rt△ABD中,由于tan∠1= ,可设AB=3m,BD=4m,利用勾股定理可知AD=5m,而H是OD中点,从而AD=
,可设AB=3m,BD=4m,利用勾股定理可知AD=5m,而H是OD中点,从而AD= AH,由于AH=6,可求AD、m的值,从而可求AB,利用∠α=∠E,再加上一个公共角,可证△ABC∽△AFE,可得比例线段,容易求出BC.
AH,由于AH=6,可求AD、m的值,从而可求AB,利用∠α=∠E,再加上一个公共角,可证△ABC∽△AFE,可得比例线段,容易求出BC.

科目:初中数学 来源: 题型:
 17、已知,如图,△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC,交AD于点M,AN平分∠DAC,交BC于点N.
17、已知,如图,△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC,交AD于点M,AN平分∠DAC,交BC于点N.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图,△ABC中,AD⊥BC,BD=DE,点E在AC的垂直平分线上.
已知:如图,△ABC中,AD⊥BC,BD=DE,点E在AC的垂直平分线上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com