
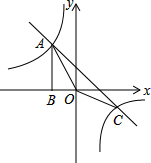
 如图,点A、点C是双曲线y1=$\frac{{k}_{1}}{x}$与直线y2=-x+k2-1的两个交点,AB⊥x轴于点B,且S△ABO=2.
如图,点A、点C是双曲线y1=$\frac{{k}_{1}}{x}$与直线y2=-x+k2-1的两个交点,AB⊥x轴于点B,且S△ABO=2.分析 (1)根据三角形ABO面积,利用反比例函数k的几何意义确定出k1的值,确定出双曲线解析式即可;
(2)①把A横坐标代入双曲线解析式确定出纵坐标,把C纵坐标代入双曲线解析式确定出横坐标,再将A坐标代入直线解析式求出k2的值,即可确定出直线解析式;
②根据A与C坐标,结合图形确定出满足题意x的范围即可.
解答 解:(1)∵点A、点C是双曲线y1=$\frac{{k}_{1}}{x}$与直线y2=-x+k2-1的两个交点,AB⊥x轴于点B,且S△ABO=2,双曲线位于第二、四象限,
∴|k1|=4,即k1=-4,
则双曲线y1的解析式为y1=-$\frac{4}{x}$;
(2)①把x=-1代入双曲线解析式得:y=4,即A(-1,4);
把y=-1代入双曲线解析式得:x=4,即C(4,-1),
把A(-1,4)坐标代入直线解析式得:4=1+k2-1,即k2=4,
则直线y2的解析式为y2=-x+3;
(3)∵A(-1,4),C(4,-1),
∴结合图形得:y1>y2时自变量x的取值范围为-1<x<0或x>4.
点评 此题考查了一次函数与反比例函数的交点问题,利用了数形结合的思想,熟练掌握一次函数与反比例函数的性质是解本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | $x-(2y-\frac{3}{2})=x-2y+\frac{3}{2}$ | B. | $-\frac{1}{2}(2x-6y+4)=-x+3y+4$ | ||
| C. | $(a+\frac{1}{2}b)-2(-\frac{1}{3}c+\frac{2}{7})=a+\frac{1}{2}b+\frac{2}{3}c-\frac{4}{7}$ | D. | m+(-n+4a-3b)=m-n+4a-3b |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,是一台自动测温记录仪记录的图象,它反映了我市春季气温T(℃)随时间t(时)变化而变化的关系,观察图象得到下列信息,其中错误的是( )
如图,是一台自动测温记录仪记录的图象,它反映了我市春季气温T(℃)随时间t(时)变化而变化的关系,观察图象得到下列信息,其中错误的是( )| A. | 凌晨4时气温最低为-5℃ | |
| B. | 14时气温最高为16℃ | |
| C. | 从0时至14时,气温随时间推移而上升 | |
| D. | 从14时至24时,气温随时间推移而下降 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{a}{b}=\frac{2}{3}$ | B. | $\frac{a+b}{a}=\frac{5}{2}$ | C. | $\frac{a+b}{a-b}=3$ | D. | $\frac{2}{a}=\frac{3}{b}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com