
����Ŀ��A��B���ع��ֱ�������40�ֺ�60�֣�C��D���طֱ���Ҫ����30�ֺ�70�֣���֪��A��B��C��D���˼������
��C�� | ��D�� | |
A�� | ÿ��15Ԫ | ÿ��12Ԫ |
B�� | ÿ��10Ԫ | ÿ��9Ԫ |
��1������A���˵�C�ص�����Ϊx�֣����A���˵�D�ص�����Ϊ �֣���A������������D�ص��������Ϊ Ԫ.
��2���ú�x��ʽ�ӱ�ʾ��������ѣ�Ҫ����ʽ������
��3��������������C�غ�D�ؽ����ټӹ��������㣬ȫ�����Ӽӹ���Ϻ��ܳɱ�ΪwԪ����![]() .��x= ʱ��w���� ֵ�����С���������ֵ�� .
.��x= ʱ��w���� ֵ�����С���������ֵ�� .
���𰸡�(1) 40-x , 12��40-x�� (2) 2x+1050 (3)25����4360.
��������
(1)����A�ع�������40����������õ�A���˵�D�ص�����Ϊ40-x��.�ɱ�����A��D�ĵ��ۣ��ٳ��Ե���12(Ԫ/ÿ��)���ɵõ�A������������D�ص��������.
(2)������x�ֱ��ʾ���˵�C�غ��˵�D�ص����Ӷ������ٷֱ���Ը��Եĵ��ۣ�������.
(3)���ݶ��κ�������ʽ![]() �Ķ�������
�Ķ�������![]() ��֪��a����0ʱ�����κ����������ϣ���
��֪��a����0ʱ�����κ����������ϣ���![]() ʱ����Сֵh��aС��0ʱ�����κ����������£���
ʱ����Сֵh��aС��0ʱ�����κ����������£���![]() ʱ�����ֵh.
ʱ�����ֵh.
(1)�������֪��A��B������������100�֣�C��D���ع���Ҫ����100��.
���A���˵�C�ص�����Ϊx�ֺ�A��ʣ�µ�����ȫ���˵�D��.
����A���˵�D�ص�����Ϊ40-x��.
�ɱ���֪����A���˵�D�ص��˷�Ϊÿ��12Ԫ.
���A������������D�ص��������Ϊ12��40-x��
(2) ��A���˵�C�ص�����Ϊx�֣�����Ϊ15x��A���˵�D�ص�����Ϊ40-x�֣�����Ϊ12��40-x��.
��ΪC��ֻ��Ҫ30�֣���C�ػ���ҪB�ص�����30-x�֣�����Ϊ10��30-x��.
ͬ����D�ػ���ҪB�ص�����70-��40-x��=30+x�֣�����Ϊ9��30+x��.
���ܷ���Ϊ��15x+12��40-x��+10��30-x��+9��30+x��=2x+1050
(3) ![]() Ϊ���κ�������ʽ
Ϊ���κ�������ʽ![]()
��ʱa=-1��0�������£������ֵ.
����x=25ʱ��w�����ֵΪ4360.
�ʴ�Ϊ��(1) 40-x , 12��40-x�� (2) 2x+1050 (3)25����4360.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+2ax+c��ͼ����x�ύ��A��B���㣨��A�ڵ�B����ߣ�AB=4����y�ύ�ڵ�C��OC=OA����DΪ�����ߵĶ��㣮
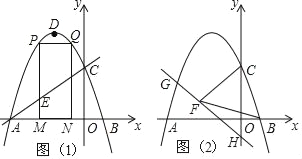
��1���������ߵĽ���ʽ��
��2����M��m��0��Ϊ�߶�AB��һ�㣨��M�����A��B�غϣ�������M��x��Ĵ��ߣ���ֱ��AC���ڵ�E���������߽��ڵ�P������P��PQ��AB���������ڵ�Q������Q��QN��x���ڵ�N���ɵþ���PQNM����ͼ1����P�ڵ�Q��ߣ�������PQNM���ܳ����ʱ����m��ֵ���������ʱ�ġ�AEM�������
��3����֪H��0����1������G���������ϣ���HG��ֱ��HG��CF������ΪF����BF=BC�����G�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ɸ�������ͬ�Ļ�������a������������ͼ�ٰڷ�ʱ�ɰڳ�m�������Σ���b������������ͼ�ڰڷ�ʱ�ɰڳ�2n�������Σ�(m��n��������)

��1����ͼ�٣���m=4ʱ��a=______����ͼ�ڣ���b=52ʱ��n=______��
��2�������ɸ�������ͬ�Ļ������ȿ��ڳ�ͼ�ٵ���״��Ҳ���ڳ�ͼ�ڵ���״ʱ��m��n֮���к�������ϵ������д������˵�����ɣ�
��3������61�������������ɸ������ڳ�ͼ�ٵ���״��ʣ�µĻ����պÿ��ڳ�ͼ�ڵ���״������ֱ��д��һ�ְڷŷ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����6��6�ķ���ֽ�У�ÿ��С�����DZ߳�Ϊ1�������Σ�����A��B��CΪ��㣬����ABC�����Բ��O����AC�ij����ڣ�������
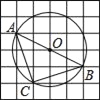
A. �� B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���![]() ��ͼ���뷴��������
��ͼ���뷴��������![]() ��ͼ����C��D���㣬 C��������ǣ�4��-1����D��ĺ�����Ϊ-2��
��ͼ����C��D���㣬 C��������ǣ�4��-1����D��ĺ�����Ϊ-2��
��1������������һ�κ����Ĺ�ϵʽ��
��2������ͼ��ֱ�ӻش𣺵�xΪ��ֵʱ��һ�κ�����ֵС�ڷ�����������ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=kx+b��ͼ��l��������ֱ��ڵ�E��F����˫����y=��![]() ��x��0�����ڵ�P����1��n������F��PE���е㣬ֱ��x=a��l���ڵ�A����˫���߽��ڵ�B����ͬ��A����PA=PB����a=________��
��x��0�����ڵ�P����1��n������F��PE���е㣬ֱ��x=a��l���ڵ�A����˫���߽��ڵ�B����ͬ��A����PA=PB����a=________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
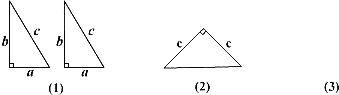
����Ŀ����ͼ(1)����Ӳֽ�����ɵ�����ȫ�ȵ�ֱ��������,��ֱ�DZߵij��ֱ�Ϊ![]() ��
��![]() б�߳�Ϊ
б�߳�Ϊ![]() ͼ(2)����
ͼ(2)����![]() Ϊֱ�DZߵĵ���ֱ��������.���㿪���Խ�,������ƴ��һ��ֱ������.
Ϊֱ�DZߵĵ���ֱ��������.���㿪���Խ�,������ƴ��һ��ֱ������.
(1)��ͼ(3)������ƴ�ɵ����ͼ�ε�ʾ��ͼ��
(2)����(1)������ͼ��֤�����ɶ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
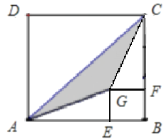
����Ŀ����ͼ��������ABCD��������BFGE�У���E�ڱ�AB�ϣ���AE=a��BE=b��������a��2b����
��1�����ú���a��b�Ĵ���ʽ��ʾͼ����Ӱ���ֵ������
��2����a=5cm��b=3cmʱ������Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y��ax2��bx��c(a��0)��ͼ��Ķ����ڵ�һ���ޣ��ҹ���(0��1)��(��1��0)�����н��ۣ���ab��0����b2��4a����0��a��b��c��2����0��b��1���ݵ�x����1ʱ��y��0.������ȷ���۵ĸ�����( )

A. 5�� B. 4�� C. 3�� D. 2��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com