
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与DB的大小关系,请你直接写出结论:AE______DB(填“>”,“<”或“=”).
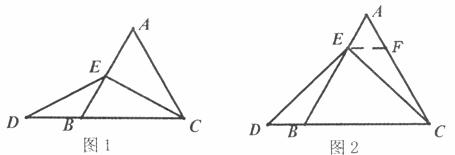
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE______DB(填“>”,“<”或“=”).
理由如下:如图2,过点E作EF∥BC,交 AC于点F.(请你补充完成解答过程)
AC于点F.(请你补充完成解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为l,AE=2,求CD的长(请你直接写出结果).
解:(1)(2分)答案为:=;
(4分)(2)答案为:=,
证明:在等边△ABC中,∠ABC=∠ACB=∠BAC=60°,
AB=BC=AC,
∵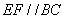 ∴∠AEF=∠ABC,∠AFE=∠ACB,
∴∠AEF=∠ABC,∠AFE=∠ACB,
∴∠AEF=∠AFE=∠BAC=60°, ∴AE=AF=EF,
∴AB﹣AE=AC﹣AF,即BE=CF,
∵∠ABC=∠EDB+∠BED=60°,∠ACB=∠ECB+∠FCE=60°,
∵ED=EC,
∴∠EDB=∠ECB,  ∵∠EBC=∠EDB+∠BED,∠ACB=∠ECB+∠FCE,
∵∠EBC=∠EDB+∠BED,∠ACB=∠ECB+∠FCE,
∴∠BED=∠FCE,
在△DBE和△EFC中 ,
,
∴△DBE≌△EFC(SAS), ∴DB=EF, ∴AE=BD;
(3)(2分)解:CD的长是3或1.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
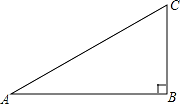
如图,在直角三角形ABC中,∠ABC=90°.
(1)先作∠ACB的平分线;设它交AB边于点O,再以点O为圆心,OB为半径作⊙O(尺规作图,保留作图痕迹,不写作法);
(2)证明:AC是所作⊙O的切线;
(3)若BC=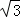 ,sinA=
,sinA=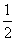 ,求△AOC的面积.
,求△AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知下列命题,其中真命题的个数是( )
①若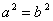 ,则
,则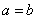 ;
;
②对角线互相垂直平分的四边形是菱形;
③两组对角分别相等的四边形是平行四边形;
④在反比例函数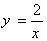 中,如果函数值y
中,如果函数值y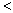 1时,那么自变量x
1时,那么自变量x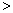 2.
2.
A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,菱形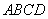 中,
中,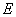 、
、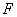 分别是边
分别是边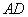 ,
,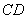 上的两个动点(不与菱形的顶点重合),且满足
上的两个动点(不与菱形的顶点重合),且满足 =
=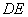 ,∠
,∠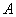 =60°.
=60°.
(1)写出图中一对全等三角形:___________________.
(2)求证:△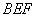 是等边三角形;
是等边三角形;
(3)若菱形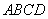 的边长为2,设△
的边长为2,设△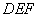 的周长为
的周长为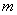 ,则
,则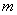 的
的 取值范围为 (直接写出答案);
取值范围为 (直接写出答案);
(4) 连接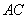 分别与边
分别与边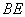 、
、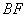 交于点
交于点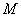 、
、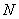 ,且∠
,且∠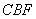 =15º,试说明:
=15º,试说明:
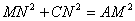 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com