练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．在Rt△ABC中，AD是斜边BC上的高，若CB=a，∠B=β，则AD等于（　　）
    A．asin2βB．acos2βC．asinβcosβD．asinβtanββ

    分析 根据题意画出图形，再由锐角三角函数的定义及三角形的面积公式即可得出结论．

    解答 解：如图所示，
    ∵在Rt△ABC中，AD是斜边BC上的高，CB=a，∠B=β，
    ∴AC=asinβ，AB=acosβ．
    ∵AD⊥BC，
    ∴BC•AD=AC•AB，即AD=$\frac{AC•AB}{BC}$=$\frac{asinβ•acosβ}{a}$=asinβcosβ．
    故选C．

    点评 本题考查的是解直角三角形，熟记锐角三角函数的定义是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

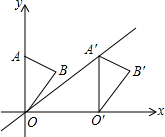    19．如图，在平面直角坐标系中，点A的坐标为（0，3），△OAB沿x轴向右平移后得到△O′A′B′，点A的对应点在直线y=$\frac{2}{3}$x上一点，则点B与其对应点B′间的距离为（　　）
    A．$\frac{2}{3}$B．$\frac{9}{2}$C．3D．5

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

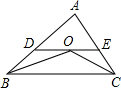    20．如图，在△ABC中，AB=6cm，AC=5cm，∠ABC与∠ACB的平分线相交于点O，过点O作DE∥BC，分别交AB，AC于点D，E，则△ADE的周长=11cm．

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年广东省梅州市七年级下学期第一次月考数学试卷（解析版） 题型：填空题

    如图，现给出下列条件：①∠1=∠B，②∠2=∠5，③∠3=∠4，④∠1=∠D，⑤∠B+∠BCD=180°，其中能够得到AB∥CD的条件是_______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．解不等式组，并把解集表示在数轴上．
    $\begin{array}{l}\left\{\begin{array}{l}2x+5≤3（x+2）\\ \frac{3}{2}x-3＜0\end{array}\right.\end{array}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．当时钟1点20分时，分针和时针之间的夹角的度数为80°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．如图，在梯形ABCD中AD∥BC，对角线AC⊥BD，且AC=12，BD=9，则AD+BC=（　　）
    A．20B．21C．15D．24

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．如果抛物线y=ax2与y=3（x+1）2-4形状相同，开口方向也相同，那么a=3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．比较大小：sin24°= cos66°，cos15°＜ tan55°．

    查看答案和解析>>

    同步练习册答案