
【题目】如图,矩形ABCD中,E是BC的中点,连接DE,P是DE上一点,∠BPC=90°,延长CP交AD于点F.⊙O经过P、D、F,交CD于点G.
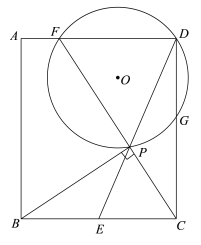
(1)求证:DF![]() DP;
DP;
(2)若![]() ,
,![]() ,求DG的长;
,求DG的长;
(3)连接BF,若BF是⊙O的切线,直接写出![]() 的值.
的值.
【答案】(1)见解析;(2)DG![]()
![]() .(3)
.(3)![]() .
.
【解析】
(1)根据题目的已知条件容易得到△DFP∽△ECP,再利用相似三角形对应边成比例即可得出结论;
(2)因为∠ADC=90°,所以FG一定是⊙O的直径,再根据弧、弦之间的关系得到∠DGF=∠DFC,进而推出△FDG∽△CDF即可得到DG的长;
(3)根据直径所对的圆周角是直角得到![]() ,P,G三点共线,再通过证明
,P,G三点共线,再通过证明![]() ∽
∽![]() 、
、![]() ∽
∽![]() 得到线段之间的比例关系,即可得到结论.
得到线段之间的比例关系,即可得到结论.
(1)证明:∵∠BPC=90°,E是BC的中点,
∴ EC![]() EP.
EP.
∵ 在矩形ABCD中,AD![]() BC,
BC,
∴ △DFP∽△ECP.
∴ ![]() .
.
即 DF![]() DP.
DP.
(2)解:连接FG.
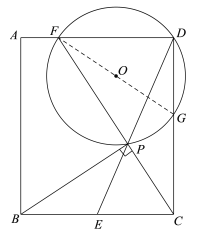
∵ 在矩形ABCD中,∠ADC=90°,
∴ FG是⊙O的直径.
∵ E是BC的中点,
∴ ![]() .
.
∵ 在矩形ABCD中,∠BCD=90°,
∴ ![]() .
.
∴ DF![]() DP
DP![]() 13-5
13-5![]() 8.
8.
∵ ⊙O中,DF![]() DP,
DP,
∴ ![]() .
.
∴ ∠DGF=∠DFC.
又 ∠FDC=∠FDC,
∴ △FDG∽△CDF.
∴ ![]() .
.
即 ![]() .
.
∴ ![]() .
.
(3)![]() .
.
如图,连接BF,FG,PG,
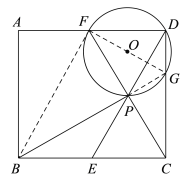
![]() 为直径,
为直径,
![]() ,
,
又![]() ,
,
![]() ,P,G三点共线,
,P,G三点共线,
![]() BF是⊙O的切线,
BF是⊙O的切线,
![]() ,
,
![]() ∽
∽![]() ,
,
![]() ,
,
由(2)已得△FDG∽△CDF,
![]() ,
,![]()
即![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ∽
∽![]() ,
,
![]() ,
,
![]() ,
,
即![]() .
.


科目:初中数学 来源: 题型:
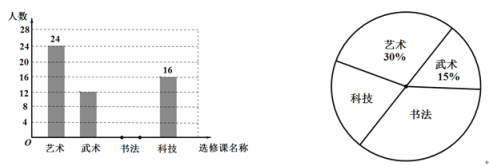
【题目】某中学进行基于学生核心素养课程体系的开发,学校计划开设:艺术、武术、书法、科技共四门选修课,并开展了以“你最想参加的选修课是哪门?(必选且只选一门选修课)”为主题的调查活动,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的统计图.请你根据统计图的信息回答下列问题:
(1)本次调查共抽取了多少名学生?
(2)分别求出参加调查的学生中选择武术和书法选修课的人数,并补全条形统计图;
(3)若该中学共有 1600 名学生,请你估计该中学选择科技选修课的学生大约有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
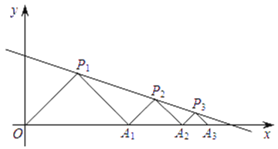
【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,
,![]() ,...都是等腰直角三角形,其直角顶点
,...都是等腰直角三角形,其直角顶点![]() ,
,![]() ,
,![]() ,...均在直线
,...均在直线![]() 上,设
上,设![]() ,
,![]() ,
,![]() ,...的面积分别为
,...的面积分别为![]() ,
,![]() ,
,![]() ,...,依据图形所反映的规律,S2020=__________.
,...,依据图形所反映的规律,S2020=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
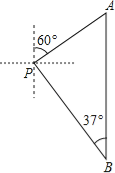
【题目】小亮一家在一湖泊中游玩,湖泊中有一孤岛,妈妈在孤岛P处观看小亮与爸爸在湖中划船(如图所示).小船从P处出发,沿北偏东60°方向划行200米到A处,接着向正南方向划行一段时间到B处.在B处小亮观测到妈妈所在的P处在北偏西37°的方向上,这时小亮与妈妈相距多少米(精确到1米)?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某篮球队员在篮球联赛中分别与甲队、乙队对阵各四场,下表是他的技术统计.
场次 | 对阵甲队 | 对阵乙队 | ||
得分(分) | 失误(次) | 得分(分) | 失误(次) | |
第一场 | 25 | 2 | 27 | 3 |
第二场 | 30 | 0 | 31 | 1 |
第三场 | 27 | 3 | 20 | 2 |
第四场 | 26 | 2 | 26 | 4 |
(1)他在对阵甲队和乙队的各四场比赛中,平均每场得分分别是多少?
(2)利用方差判断他在对阵哪个队时得分比较稳定;
(3)根据上表提供的信息,判断他在对阵哪个队时总体发挥较好,简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D为边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE点F在AB上,且BF=DE
(1)求证:四边形BDEF是平行四边形
(2)线段AB,BF,AC之间具有怎样的数量关系?证明你所得到的结论

查看答案和解析>>
科目:初中数学 来源: 题型:
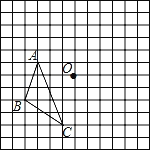
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点![]() ABC(顶点是网格线的交点)和格点O.
ABC(顶点是网格线的交点)和格点O.
(1)平移![]() ABC,使得点A与点O重合,画出平移后的
ABC,使得点A与点O重合,画出平移后的![]() A′B′C′;
A′B′C′;
(2)画出![]() ABC关于点O对称的
ABC关于点O对称的![]() DEF;
DEF;
(3)判断![]() A′B′C′与
A′B′C′与![]() DEF是否成中心对称?
DEF是否成中心对称?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于A,B两点(点A在点B的左侧),直线
轴交于A,B两点(点A在点B的左侧),直线![]() 与抛物线交于
与抛物线交于![]() 两点,其中点
两点,其中点![]() 的横坐标为2.
的横坐标为2.
(1)求A,B两点的坐标及直线AC的表达式;
(2)P是线段AC上一动点(P与A,C不重合),过点P作![]() 轴的平行线交抛物线于点E,求
轴的平行线交抛物线于点E,求![]() 面积的最大值;
面积的最大值;
(3)点H是抛物线上一动点,在![]() 轴上是否存在点F,使得
轴上是否存在点F,使得![]() 四个点为顶点的四边形是平行四边形?如果存在请直接写出所有满足条件的点F坐标;如果不存在,请说明理由.
四个点为顶点的四边形是平行四边形?如果存在请直接写出所有满足条件的点F坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,单位长度为![]() 的网格坐标系中,一次函数
的网格坐标系中,一次函数![]() 与坐标轴交于
与坐标轴交于![]() 、
、![]() 两点,反比例函数
两点,反比例函数![]()
![]() 经过一次函数上一点
经过一次函数上一点![]() .
.
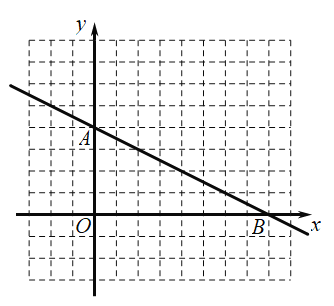
(1)求反比例函数解析式,并用平滑曲线描绘出反比例函数图像;
(2)依据图像直接写出当![]() 时不等式
时不等式![]() 的解集;
的解集;
(3)若反比例函数![]() 与一次函数
与一次函数![]() 交于
交于![]() 、
、![]() 两点,在图中用直尺与
两点,在图中用直尺与![]() 铅笔画出两个矩形(不写画法),要求每个矩形均需满足下列两个条件:
铅笔画出两个矩形(不写画法),要求每个矩形均需满足下列两个条件:
①四个顶点均在格点上,且其中两个顶点分别是点![]() 、点
、点![]() ;
;
②矩形的面积等于![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com