
【题目】如图,已知AC是⊙O的直径,B为⊙O上一点,D为![]() 的中点,过D作EF∥BC交AB的延长线于点E,交AC的延长线于点F.
的中点,过D作EF∥BC交AB的延长线于点E,交AC的延长线于点F.
(Ⅰ)求证:EF为⊙O的切线;
(Ⅱ)若AB=2,∠BDC=2∠A,求![]() 的长.
的长.

【答案】(1)详见解析;(2)![]()
【解析】
(Ⅰ)连接OD,OB,只要证明OD⊥EF即可;
(Ⅱ)根据已知结合圆内接四边形的性质得出∠A=60°,即可得出△OAB等边三角形,再利用弧长公式计算得出答案.
(1)连接OD,OB,

∵D为![]() 的中点,
的中点,
∴∠BOD=∠COD,
∵OB=OC,
∴OD⊥BC,
∴∠OGC=90°,
∵EF∥BC,
∴∠ODF=∠OGC=90°,
即OD⊥EF,
∵OD是⊙O的半径,
∴EF是⊙O的切线;
(2)∵四边形ABDC是⊙O的内接四边形,
∴∠A+∠BDC=180°,
又∵∠BDC=2∠A,
∴∠A+2∠A=180°,
∴∠A=60°,
∵OA=OB,
∴△OAB 等边三角形,
∵OB=AB=2,
又∵∠BOC=2∠A=120°,
∴EC=![]() .
.


科目:初中数学 来源: 题型:
【题目】小刚很擅长球类运动,课外活动时,足球队、篮球队都力邀他到自己的阵营,小刚左右为难,最后决定通过掷硬币来确定。游戏规则如下:连续抛掷硬币三次,如果三次正面朝上或三次反面朝上,则由小刚任意挑选两球队;如果两次正面朝上一次正面朝下,则小刚加入足球阵营;如果两次反面朝上一次反面朝下,则小刚加入篮球阵营。
(1)用画树状图的方法表示三次抛掷硬币的所有结果。
(2)小刚任意挑选两球队的概率有多大?
(3)这个游戏规则对两个球队是否公平?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】投资1万元围一个矩形菜园(如图),其中一边靠墙,另外三边选用不同材料建造.墙长24 m,平行于墙的边的费用为200元/m,垂直于墙的边的费用为150元/m,设平行于墙的边长为x m.
(1)设垂直于墙的一边长为y m,直接写出y与x之间的函数关系式;
(2)若菜园面积为384 m2,求x的值;
(3)求菜园的最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程(k﹣1)x2+(2k﹣3)x+k+1=0有两个不相等的实数根.
(1)求k的取值范围;
(2)如果k是符合条件的最大整数,且一元二次方程x2﹣4x+k=0与x2+mx﹣1=0有一个相同的根,求此时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,CD为AB边上中线,E是CB边上的一个动点.
,CD为AB边上中线,E是CB边上的一个动点.
![]() Ⅰ
Ⅰ![]() 求CD的长;
求CD的长;
![]() Ⅱ
Ⅱ![]() 如图1,连接AE,交CD于点F,当AE平分
如图1,连接AE,交CD于点F,当AE平分![]() 时,求CE,CF的长;
时,求CE,CF的长;
![]() Ⅲ
Ⅲ![]() 如图2,连接DE,将
如图2,连接DE,将![]() 沿DE翻折至
沿DE翻折至![]() ,连接BG,直接写出
,连接BG,直接写出![]() 和
和![]() 间的数量关系.
间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)如图,AB是![]() 的直径,且
的直径,且![]() ,点M为
,点M为![]() 外一点,且MA,MC分别切
外一点,且MA,MC分别切![]() 于点A、C两点
于点A、C两点![]() 与AM的延长线交于点D.
与AM的延长线交于点D.
![]() 求证:
求证:![]() ;
;
![]() 填空
填空
![]() 当
当![]() ______时,四边形AOCM是正方形.
______时,四边形AOCM是正方形.
![]() 当
当![]() ______时,
______时,![]() 为等边三角形.
为等边三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
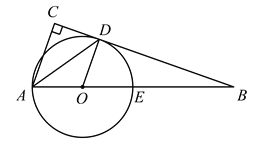
【题目】如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC交BC于点D,点O是AB边上一点,以O为圆心作⊙O且经过A,D两点,交AB于点E.
(1)求证:BC是⊙O的切线;
(2)AC=2,AB=6,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
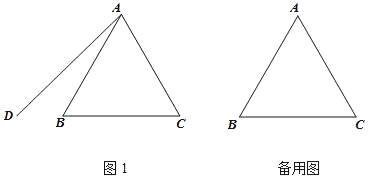
【题目】在等边△ABC外作射线AD,使得AD和AC在直线AB的两侧,∠BAD=α(0°<α<180°),点B关于直线AD的对称点为P,连接PB,PC.
(1)依题意补全图1;
(2)在图1中,求△BPC的度数;
(3)直接写出使得△PBC是等腰三角形的α的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com