
【题目】如图,一次函数y=kx+b与反比例函数![]() 的图像交于A(2,4),B(-4,n)两点,交x轴于点C.
的图像交于A(2,4),B(-4,n)两点,交x轴于点C.

(1)求m、n的值;
(2)请直接写出不等式kx+b<![]() 的解集;
的解集;
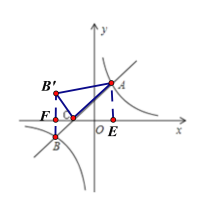
(3)将x轴下方的图像沿x轴翻折,点B落在点B′处,连接AB′、B′C,求△A B′C的面积.
【答案】(1)m=8,n=-2 ;(2)x<-4或0<x<2 ;(3)8
【解析】(1)先求出![]() ,再把B(-4,n)代入得
,再把B(-4,n)代入得![]() ;(2)结合图形求解;(3)用待定系数法求直线解析式,再求C的坐标,同时求B′的坐标,根据坐标求三角形面积.
;(2)结合图形求解;(3)用待定系数法求直线解析式,再求C的坐标,同时求B′的坐标,根据坐标求三角形面积.
解:(1)把A(2,4)代入![]() ,得
,得![]() ,解得m=8,
,解得m=8,
所以,![]() ,把B(-4,n)代入得
,把B(-4,n)代入得![]() ,解得n=-2,
,解得n=-2,
(2)由图形可知不等式kx+b<![]() 的解集:x<-4或0<x<2;
的解集:x<-4或0<x<2;
(3)
把A(2,4),B(-4,-2)分别代入y=kx+b,得
![]()
解得
![]() ,
,
所以,![]()
当y=0时,x=-2
所以,C(-2,0)
作AE⊥x轴,连接BB′与x轴交F
由已知得B′(-4,2),
所以,△A B′C的面积=S梯形AEFB′-S△ B′FC-S△ACE
=![]()


科目:初中数学 来源: 题型:
【题目】如图,在直角∠O的内部有一滑动杆AB,当端点A沿直线AO向下滑动时,端点B会随之自动地沿直线OB向左滑动,如果滑动杆从图中AB处滑动到A′B′处,那么滑动杆的中点C所经过的路径是( ) 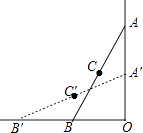
A.直线的一部分
B.圆的一部分
C.双曲线的一部分
D.抛物线的一部分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c与x轴的一个交点为A(3,0),与y轴的交点为B(0,3),其顶点为C,对称轴为x=1.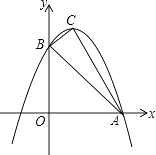
(1)求抛物线的解析式;
(2)已知点M为y轴上的一个动点,当△ABM为等腰三角形时,求点M的坐标;
(3)将△AOB沿x轴向右平移m个单位长度(0<m<3)得到另一个三角形,将所得的三角形与△ABC重叠部分的面积记为S,用m的代数式表示S.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图甲,在△ABC中,∠ACB=90°,AC=4cm,BC=3cm.如果点P由点B出发沿BA方向向点A匀速运动,同时点Q由点A出发沿AC方向向点C匀速运动,它们的速度均为1cm/s.连接PQ,设运动时间为t(s)(0<t<4),解答下列问题: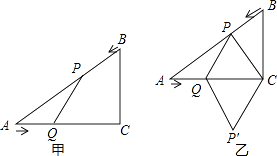
(1)设△APQ的面积为S,当t为何值时,S取得最大值?S的最大值是多少?
(2)如图乙,连接PC,将△PQC沿QC翻折,得到四边形PQP′C,当四边形PQP′C为菱形时,求t的值;′
(3)当t为何值时,△APQ是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
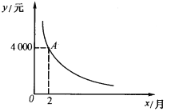
【题目】李先生参加了某电脑公司推出的分期付款购买电脑活动,他购买的电脑价格为1.2万元,交了首付4000元之后每期付款y元,x个月结清余款.
(1)写出y与x的函数关系式.
(2)如打算每月付款不超过500元,李先生至少几个月才能结清余款?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是(A,B)的妙点.
例如,如图1,点A表示的数为﹣1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是(A,B)的妙点;又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D就不是(A,B)的妙点,但点D是(B,A)的妙点.
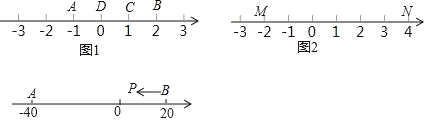
知识运用:如图2,M、N为数轴上两点,点M所表示的数为﹣2,点N所表示的数为4.
(1)数 所表示的点是(M,N)的妙点;
(2)如图3,A、B为数轴上两点,点A所表示的数为﹣40,点B所表示的数为20.现有一只电子蚂蚁P从点B出发向左运动,到达点A停止.P点运动多少个单位时,P、A和B中恰有一个点为其余两点的妙点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD和四边形AECF都是矩形,AE与BC交于点M,CF与AD交于点N.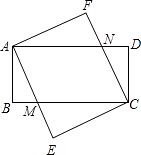
(1)求证:△ABM≌△CDN;
(2)矩形ABCD和矩形AECF满足何种关系时,四边形AMCN是菱形,证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家超市进行促销活动,甲超市采用“买100减50”的促销方式,即购买商品的总金额满100元但不足200元,少付50元;满200元但不足300元,少付100元;….乙超市采用“打6折”的促销方式,即顾客购买商品的总金额打6折.
(1)若顾客在甲商场购买商品的总金额为x(100≤x<200)元,优惠后得到商家的优惠率为p(p= ![]() ),写出p与x之间的函数关系式,并说明p随x的变化情况;
),写出p与x之间的函数关系式,并说明p随x的变化情况;
(2)王强同学认为:如果顾客购买商品的总金额超过100元,实际上甲超市采用“打5折”、乙超市采用“打6折”,那么当然选择甲超市购物.请你举例反驳;
(3)品牌、质量、规格等都相同的某种商品,在甲乙两商场的标价都是x(300≤x<400)元,认为选择哪家商场购买商品花钱较少?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com