
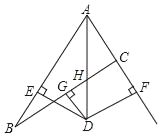
【题目】如图,在△ABC中,AD平分∠BAC,DG⊥BC且平分BC于点G,DE⊥AB于点E,DF⊥AC交AC的延长线于点F.
(1)求证:AE=AF;
(2)求证:BE=CF;
(3)如果AB=12,AC=8,求AE的长.
【答案】(1)见解析;(2)见解析;(3)10.
【解析】
(1)根据角平分线的性质解答即可;
(2)连接DB、DC,证明Rt△BDE≌Rt△CFD即可得出结论;
(3)由(2)可得出CF=BE,且AE=AF=AC+CF,而CF=BE=AB-AE,代入可求得结果.
证明:(1)∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴AE=AF;
(2)连接DB、DC,
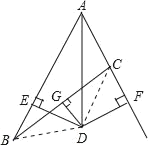
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,
∵DG⊥BC且平分BC于点G,
∴DB=DC,
在Rt△BDE和Rt△CFD中,
![]() ,
,
∴Rt△BDE≌Rt△CDF(HL),
∴BE=CF;
(3)由(2)知BE=CF,
且在△ADE和△ADF中
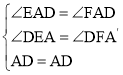
∴△ADE≌△ADF(AAS),
∴AE=AF=AC+CF,
而CF=BE=AB﹣AE,
∴AE=AC+AB﹣AE,
∴2AE=AC+AB=8+12=20,
∴AE=10.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,长方形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边的中点,点
边的中点,点![]() 从点
从点![]() 出发,沿着
出发,沿着![]() 方向运动再过点
方向运动再过点![]() 沿
沿![]() 方向运动,到点
方向运动,到点![]() 停止运动,点
停止运动,点![]() 以同样的速度从点
以同样的速度从点![]() 出发沿着
出发沿着![]() 方向运动,到点
方向运动,到点![]() 停止运动,设点
停止运动,设点![]() 运动的路程为
运动的路程为![]() .
.
(1)当![]() 时,线段
时,线段![]() 的长是 ;
的长是 ;
(2)当点![]() 在线段
在线段![]() 上运动时,图中阴影部分的面积会发生改变吗?请你作出判断并说明理由.
上运动时,图中阴影部分的面积会发生改变吗?请你作出判断并说明理由.
(3)在点![]() 的运动过程中,是否存在某一时刻,使得
的运动过程中,是否存在某一时刻,使得![]() ?若存在,求出点
?若存在,求出点![]() 的运动路程,若不存在,请说明理由.
的运动路程,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠A=90°,点P.Q分別是AB、AC上的动点,且满足BP=AQ,D是BC的中点,当点P运动到___时,四边形APDQ是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,直线![]() 与反比例函数
与反比例函数![]() 交于点
交于点![]() ,且点
,且点![]() 的横坐标为4,过
的横坐标为4,过![]() 轴上一点
轴上一点![]() 作
作![]() 垂直于
垂直于![]() 交
交![]() 于
于![]() 点,如图.
点,如图.

(1)若点![]() 是线段
是线段![]() 上一动点,过点
上一动点,过点![]() 作
作![]() ,
,![]() ,垂足分别于
,垂足分别于![]() 、
、![]() ,求线段
,求线段![]() 长度的最小值.
长度的最小值.
(2)在(1)的![]() 取得最小值的前提下,将
取得最小值的前提下,将![]() 沿射线
沿射线![]() 平移,记平移后的三角形为
平移,记平移后的三角形为![]() ,当
,当![]() 时,在平面内存在点
时,在平面内存在点![]() ,使得
,使得![]() 、
、![]() 、
、![]() 、
、![]() 四点构成平行四边形,这样的点
四点构成平行四边形,这样的点![]() 有几个?直接写出点
有几个?直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励居民节约用电,国家发改委发布文件在全国实行“阶梯电价”收费,重庆结合本市实际,根据国家发改委文件要求,决定从2016年1月1日起对居民生活用电实行“阶梯电价”收费,具体收费标准见下表.若2016年8月份,该市居民甲生活用电240千瓦时(能量量度单位,1千瓦时即1度),交电费130元.
一户居民一个月用电量 | 电费价格(元/千瓦时) | |
第一档 | 不超过200千瓦时 | 0.52 |
第二档 | 超过200千瓦时但不超过320千瓦时 |
|
第三档 | 超过320千瓦时 | 0.95 |
(1)求上表中的![]() 的值;
的值;
(2)若该市居民乙某月交电费220元,居民乙当月的生活用电量为多少千瓦时?
(3)实行“阶梯电价”收费后,该市居民丙月用电量为多少千瓦时,其当月的平均电价为0.55元/千瓦时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=12,点D在边BC上,点E在线段AD上,EF⊥AC于点F,EG⊥EF交AB于点G,若EF=EG,则CD的长为( )
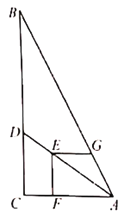
A.3.6B.4C.4.8D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】类比探究:
(1)如图1,等边△ABC内有一点P,若AP=8,BP=15,CP=17,求∠APB的大小;(提示:将△ABP绕顶点A旋转到△ACP′处)
(2)如图2,在△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点,且∠EAF=45°.求证:EF2=BE2+FC2;
(3)如图3,在△ABC中,∠C=90°,∠ABC=30°,点O为△ABC内一点,连接AO、BO、CO,且∠AOC=∠COB=∠BOA=120°,若AC=1,求OA+OB+OC的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用“*”定义一种新运算:对于任意有理数a和b,规定a*b=ab2+2ab+a.
如:1*3=1×32+2×1×3+1=16
(1)求2*(﹣2)的值;
(2)若2*x=m,![]() (其中x为有理数),试比较m,n的大小;
(其中x为有理数),试比较m,n的大小;
(3)若[![]() ]
]![]() =a+4,求a的值.
=a+4,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com