
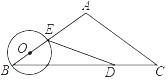
【题目】如图,等腰△ABC中,AB=AC=5cm,BC=8cm.动点D从点C出发,沿线段CB以2cm/s的速度向点B运动,同时动点O从点B出发,沿线段BA以1cm/s的速度向点A运动,当其中一个动点停止运动时另一个动点也随时停止.设运动时间为t(s),以点O为圆心,OB长为半径的⊙O与BA交于另一点E,连接ED.当直线DE与⊙O相切时,t的取值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:
【题目】已知矩形AOBC的边AO、OB分别在y轴、x轴正半轴上,点C的坐标为(8,6),点E是x轴上任意一点,连接EC,交AB所在直线于点F,当△ACF为等腰三角形时,EF的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
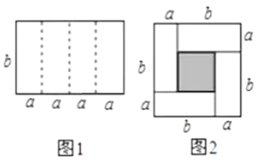
【题目】探究:(1)如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图2),请你写出![]() 、
、![]() 、ab之间的等量关系是______________;
、ab之间的等量关系是______________;
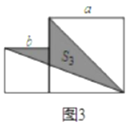
(2)两个边长分别为a和b的正方形如图放置(图3),求出图3中阴影部分的面积![]() ;
;
(3)若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线L: ![]() (常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线
(常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线![]() 于点P,且OA·MP=12.
于点P,且OA·MP=12.
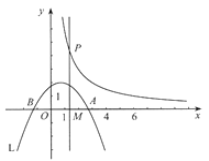
(1)求k值;
(2)当t=1时,求AB长,并求直线MP与L对称轴之间的距离;
(3)把L在直线MP左侧部分的图象(含与直线MP的交点)记为G,用t表示图象G最高点的坐标;
(4)设L与双曲线有个交点的横坐标为x0,且满足4≤x0≤6,通过L位置随t变化的过程,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个几何体的俯视图,则这个几何体的形状可能是( )
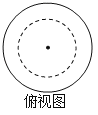
A.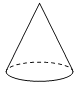 B.[Failed to download image : http://192.168.0.10:8086/QBM/2020/6/21/2489183741517824/2490750925307904/STEM/789274b5f2a548a49af6fc88629e8cdc.png] C.
B.[Failed to download image : http://192.168.0.10:8086/QBM/2020/6/21/2489183741517824/2490750925307904/STEM/789274b5f2a548a49af6fc88629e8cdc.png] C.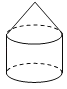 D.
D.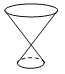
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,AB=AC,∠BAC=α,直线l经过点A(不经过点B或点C),点C关于直线l的对称点为点D,连接BD,CD.
(1)如图1,
①求证:点B,C,D在以点A为圆心,AB为半径的圆上.
②直接写出∠BDC的度数(用含α的式子表示)为______.
(2)如图2,当α=60°时,过点D作BD的垂线与直线l交于点E,求证:AE=BD.
(3)如图3,当α=90°时,记直线l与CD的交点为F,连接BF.将直线l绕点A旋转,当线段BF的长取得最大值时,直接写出tan∠FBC的值.
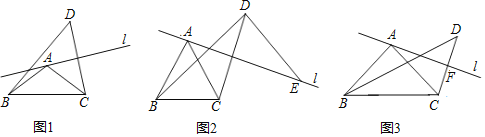
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC中,AB=AC.
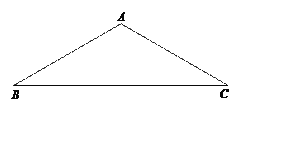
(1)用尺规作出圆心在直线BC上,且过A、C两点的⊙O;(注:保留作图痕迹,标出点O,并写出作法)
(2)若∠B=30°,求证:AB与(1)中所作⊙O相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=25°,O为AB的中点. 将OA绕点O逆时针旋转θ °至OP(0<θ<180),当△BCP恰为轴对称图形时,θ的值为_____________.
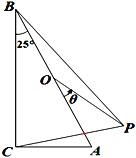
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com