
����Ŀ��������ȫ�ȵĺ�30���ǵ�ֱ�����ǰ尴��ͼ1��ʾ�ķ�ʽ���ã���֪��BAC����B1A1C��30�����̶����ǰ�A1B1C��Ȼ�����ǰ�ABC��ֱ�Ƕ���C˳ʱ����ת����ת��С��90��������ͼ2��ʾ��λ�ã�AB��A1C��A1B1�ֱ��ڵ�D��E��AC��A1B1���ڵ�F��
��1������ת�ǵ���20��ʱ����BCB1���� ������
��2������ת�ǵ��ڶ��ٶ�ʱ��AB��A1B1��ֱ����˵�����ɣ�

���𰸡���1��160����2������ת�ǵ���30��ʱ��AB��A1B1��ֱ�����ɼ�������
��������
��1����ת�ǡ�A1CA��20�㣬���ԡ�BCB1��90�㣫90��20�㣽160�㣻
��2����AB��A1B1��ֱʱ����A1ED��90�㣬������A1DE����������������������ʿ�֪��DCA����������ת�Ƕ�����
�⣺��1������ת�ǵ���20��ʱ�����A1CA��20����
���BCB1��90��+90����20����160����
�ʴ�Ϊ160��
��2������ת�ǵ���30��ʱ��AB��A1B1��ֱ���������£�
��AB��A1B1��ֱʱ����A1ED��90��
���A1DE��90������A1��90����30����60����
�ߡ�A1DE����A+��DCA��
���DCA��60����30����30����
������ת�ǵ���30��ʱ��AB��A1B1��ֱ��
�ʴ�Ϊ160��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCO�ı�OC��x����������ϣ���OA��y����������ϣ�����������y��![]() ��k��0���ڵ�һ����ͼ����Խ���OB���е�D������BC�ڵ�E������E��EG��OB��x���ڵ�F����y���ڵ�G������B�������ǣ�8��6�������ı���OBEG���ܳ���_____��
��k��0���ڵ�һ����ͼ����Խ���OB���е�D������BC�ڵ�E������E��EG��OB��x���ڵ�F����y���ڵ�G������B�������ǣ�8��6�������ı���OBEG���ܳ���_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���BAC=90������DΪBC�е㣬����ABD�Ƶ�A����ʱ�뷽����ת50�����ǵ�D����ת��������������·����Ϊm������ABD�Ƶ�C��˳ʱ�뷽����ת100�������D����ת��������������·����Ϊ________.(�ú�m�Ĵ���ʽ��ʾ)

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����Rt��ABC�У���A��90�㣬AB��AC����D��E�ֱ��ڱ�AB��AC�ϣ�AD��AE������DC����M��P��N�ֱ�ΪDE��DC��BC���е㣮
��1���۲����
ͼ1�У��߶�PM��PN��������ϵ���� ����λ�ù�ϵ���� ����
��2��̽��֤��
�ѡ�ADE�Ƶ�A��ʱ�뷽����ת��ͼ2��λ�ã�����MN��BD��CE���жϡ�PMN����״����˵�����ɣ�
��3����չ����
�ѡ�ADE�Ƶ�A��ƽ����������ת����AD��4��AB��10����ֱ��д����PMN��������ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=ax2+bx+c�Ķ���ΪD���C1��2������x���һ������A�ڵ㣨�C3��0���ͣ��C2��0��֮�䣬�䲿��ͼ������ͼ�������½��ۣ���b2�C4ac<0����a+b+c<0����c�Ca=2���ܷ���ax2+bx+c�C2=0��������ȵ�ʵ������������ȷ���۵ĸ���Ϊ�� ��
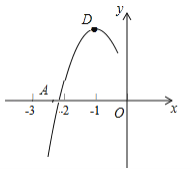
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() �У�
��![]() ��
��![]() ��
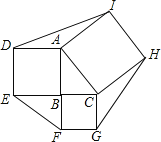
��![]() �������߷ֱ����������������Σ����Ӹ��㣬�õ�������DEFGHI����������DEFGHI�����Ϊ________��
�������߷ֱ����������������Σ����Ӹ��㣬�õ�������DEFGHI����������DEFGHI�����Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ÿ���![]() ��
��![]() ��Ϊ���绷���գ�Ϊ���ᳫ��̼������ij��˾��������
��Ϊ���绷���գ�Ϊ���ᳫ��̼������ij��˾��������![]() ̨��ʡ��Դ�����豸�����мס��������ͺŵ��豸�ɹ�ѡ��.�����飺����
̨��ʡ��Դ�����豸�����мס��������ͺŵ��豸�ɹ�ѡ��.�����飺����![]() ̨�����豸�ȹ���
̨�����豸�ȹ���![]() ̨�����豸�
̨�����豸�![]() ��Ԫ������
��Ԫ������![]() ̨�����豸�ȹ���
̨�����豸�ȹ���![]() ̨�����豸�ٻ�
̨�����豸�ٻ�![]() ��Ԫ.
��Ԫ.
��1����ס��������ͺ��豸ÿ̨�ļ۸�
��2���ù�˾��������������豸������![]() ̨��Ԥ�㹺���ʡ��Դ�����豸�ʽ���
̨��Ԥ�㹺���ʡ��Դ�����豸�ʽ���![]() ��Ԫ������Ϊ�ù�˾���ļ��ֹ�����
��Ԫ������Ϊ�ù�˾���ļ��ֹ�����
��3���ڣ�2���������£���֪�����豸ÿ�µIJ���Ϊ![]() �֣������豸ÿ�µIJ���Ϊ
�֣������豸ÿ�µIJ���Ϊ![]() ��.��ÿ��Ҫ�����������
��.��ÿ��Ҫ�����������![]() �֣�Ϊ�˽�Լ�ʽ�����Ϊ�ù�˾���һ����ʡǮ�Ĺ���.
�֣�Ϊ�˽�Լ�ʽ�����Ϊ�ù�˾���һ����ʡǮ�Ĺ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��l��x���ཻ�ڵ�M��3��0������y���ཻ�ڵ�N��0��4������AΪMN���е㣬����������y=![]() ��x��0����ͼ�����A��
��x��0����ͼ�����A��
��1����ֱ��l�ͷ����������Ľ���ʽ��
��2���ں���y=![]() ��k��0����ͼ����ȡ���ڵ�A��һ��C����CB��x���ڵ�B������OC��ֱ��l�ڵ�P������ONP������ǡ�OBC�����3�������P�����꣮
��k��0����ͼ����ȡ���ڵ�A��һ��C����CB��x���ڵ�B������OC��ֱ��l�ڵ�P������ONP������ǡ�OBC�����3�������P�����꣮

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com