Question

3．如图，直角梯形ABCD中，AB∥CD，∠A=90°，CD=3，AD=4，tanB=2，过点C作CH⊥AB，垂足为H．点P为线段AD上一动点，直线PM∥AB，交BC、CH于点M、Q．设PD的长为x．
（1）求PM的长（用x表示）；
（2）若以PM为直径的⊙O恰好过点C时，求x的值；
（3）若以PM为斜边向下作等腰Rt△PMN，直线MN交直线AB于点E．当点E在线段AH上时，求x的取值范围． 

Answer 1

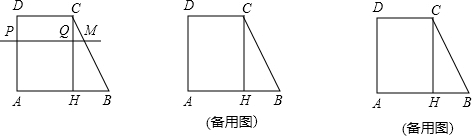
分析 （1）已知了PD的长为x，即CQ=x，结合∠B的正切值即可求得MQ的长，进而由PM=PQ+MQ求得PD表达式．
（2）利用圆周角定理得到∠PCM=90°，所以在直角△PCM中，利用射影定理来求x的值即可．
（3）首先由E、A重合时求得求得KH的表达式，当E从A移动到H时，此时K也与H重合，由此可得KH的取值范围，联立KH的表达式即可得到x的取值范围．

解答 解：（1）如图1，∵∠A=90°，CH⊥AB，
∴CH∥AD，
∵CD∥AB，
∴四边形CHAD是矩形，
∴CD=AH=3=PQ，CH=AD=4，
∵tanB=2=$\frac{CH}{BH}$，
∴BH=2，
∵PQ∥AB，
∴$\frac{QM}{BH}$=$\frac{CQ}{CH}$=$\frac{PD}{AD}$，
即$\frac{QM}{2}$=$\frac{m}{4}$，
∴OM=$\frac{1}{2}$x，
∴PM=3+$\frac{1}{2}$x．
答：PM的长是3+$\frac{1}{2}$x．

（2）如图2，连接PC．
∵PM是直径，
∴∠PCM=90°，
又∵CQ⊥PM，
∴CQ²=PQ•QM，即x²=3×$\frac{1}{2}$x，
解得x=1.5；

（3）如图3，当E、A重合时，AH=HK=3，QM=QK=$\frac{x}{2}$；
∴HK=AP-QK=（4-x）-$\frac{1}{2}$x=4-$\frac{3}{2}$x，
当点E从点A移动到点H时，K与H重合，即0≤KH≤3；
∴0≤4-$\frac{3}{2}$x≤3，
解得：$\frac{2}{3}$≤x≤$\frac{8}{3}$；
即当点E在线段AH上时，x的取值范围是 $\frac{2}{3}$≤x≤$\frac{8}{3}$．

点评 此题主要考查了四边形综合题，解题时需要用到直角梯形、等腰直角三角形、矩形的性质以及锐角三角函数的定义等知识，在涉及动点问题时，一定要注意分类讨论思想的运用，以免漏解．