
分析 (1)根据待定系数法即可求出这个函数的解析式
(2)将抛物线的解析式即可求出顶点坐标.
(3)求出抛物线与x轴、y轴的交点坐标即可求出三角形的面积.
解答 解:(1)设抛物线的解析式为y=a(x-h)2+k
∵B、C的纵坐标都是-4,
∴B、C关于抛物线的对称轴对称,
∴抛物线的对称轴为:x=1,
即h=1,
∴y=a(x-1)2+k,
将A(4,0)和B(0,-4)代入上式,
$\left\{\begin{array}{l}{9a+k=0}\\{a+k=-4}\end{array}\right.$
解得:$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{k=-\frac{9}{2}}\end{array}\right.$
∴抛物线的解析式为:y=$\frac{1}{2}$(x-1)2-$\frac{9}{2}$
(2)由(1)可知:顶点坐标为(1,-$\frac{9}{2}$)
(3)令y=0代入y=$\frac{1}{2}$(x-1)2-$\frac{9}{2}$,
∴抛物线与x轴的交点坐标为:(4,0)或(-2,0)
∵抛物线与y轴的交点坐标为:(0,-4)
∴抛物线与坐标轴的交点围成的三角形的面积为:$\frac{1}{2}$×6×4=12
点评 本题考查二次函数综合问题,解题的关键是根据三点的坐标求出抛物线的解析式,本题属于基础题型.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 某商场“五一”期间为进行有奖销售活动,设立了一个可以自由转动的转盘,商场规定:顾客购物100元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是此次活动中的一组统计数据:
某商场“五一”期间为进行有奖销售活动,设立了一个可以自由转动的转盘,商场规定:顾客购物100元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是此次活动中的一组统计数据:| 转动转盘的次数n | 100 | 200 | 400 | 500 | 800 | 1000 |
| 落在“可乐”区域的次数m | 60 | 122 | 240 | 298 | 476 | 604 |
| 落在“可乐”区域的频率$\frac{m}{n}$ | 0.6 | 0.61 | 0.6 | 0.6 | 0.59 | 0.604 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ∠A=30°、∠B=60° | B. | ∠A=50°、∠B=80° | ||
| C. | ∠A=2∠B=70° | D. | AB=4、BC=5、周长为15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
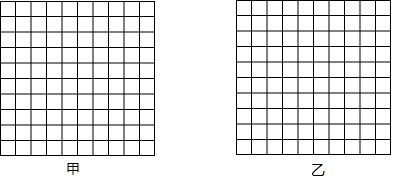
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
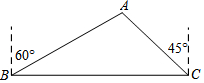 如图,一艘轮船自西向东航行,在点B处测得北偏东60°方向有一灯塔A,继续向东航行40海里到达C处,测得灯塔A在点C的北偏西45°方向上,求轮船行至点C处时,轮船与灯塔A的距离AC为多少海里?
如图,一艘轮船自西向东航行,在点B处测得北偏东60°方向有一灯塔A,继续向东航行40海里到达C处,测得灯塔A在点C的北偏西45°方向上,求轮船行至点C处时,轮船与灯塔A的距离AC为多少海里?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 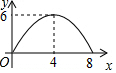 | B. | 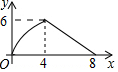 | C. | 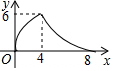 | D. | 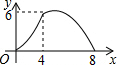 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com