
【题目】在△ABC中,![]() ,AC=4,BC=3,点D是斜边AB的中点. 以点D为顶点作
,AC=4,BC=3,点D是斜边AB的中点. 以点D为顶点作![]() ,射线DM、DN分别交边AC、CB于点E、F.
,射线DM、DN分别交边AC、CB于点E、F.

特例
(1)如图1,若![]() ,不添加辅助线,图1中所有与△ABC相似的三角形为 ,
,不添加辅助线,图1中所有与△ABC相似的三角形为 ,![]() ;
;
操作探究:
(2)将(1)中的![]() 从图1 的位置开始绕点D按逆时针方向旋转,得到
从图1 的位置开始绕点D按逆时针方向旋转,得到![]() .如图2,当射线
.如图2,当射线![]() 分别交边
分别交边![]() 于点
于点![]() 时,求
时,求![]() 的值;
的值;
拓展延伸:
(3)如图3,![]() 中,
中,![]() ,AC=m,BC=n,点D是斜边AB的中点,以点D为顶点作
,AC=m,BC=n,点D是斜边AB的中点,以点D为顶点作![]() ,射线
,射线![]() 分别交边
分别交边![]() 的延长线于点
的延长线于点![]() ,则
,则![]() 的值为_______________.(用含
的值为_______________.(用含![]() 的代数式表示,直接回答即可)
的代数式表示,直接回答即可)
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)证得四边形DECF为矩形,则DF∥AC,则![]() ,
,![]() ,又根据三角形中位线的性质,即可求得
,又根据三角形中位线的性质,即可求得![]() 的值;
的值;
(2)由旋转可知∠![]() ∠
∠![]() ,可证得
,可证得![]() ,由(1)的结论可求得答案;
,由(1)的结论可求得答案;
(3)作DG⊥AC于G,DH⊥BC于H,利用三角形中位线定理求得![]() ,
,![]() ,再证得
,再证得![]() ,即可求解.
,即可求解.
(1)∵DE∥BC,∠ACB=∠EDF=![]() ,
,
∴四边形DECF为矩形,
∴DF∥AC,
∴![]() ,
,![]() ;
;
∵点D是斜边AB的中点,
∴![]() ,
,![]() ,
,
∴![]() ,
,
故答案为:![]() ,
,![]() ,
,![]() ;
;
(2)由旋转可知:∠![]() ∠
∠![]() ,且∠
,且∠![]() ∠
∠![]() ,
,
∴![]() ,
,
∴![]() ,
,
由(1)得![]() ,
,
∴![]() ;
;
(3)作DG⊥AC于G,DH⊥BC于H,
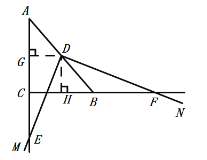
∵点D是斜边AB的中点,
∴![]() ,
,![]() ,
,
∵DG⊥AC,DH⊥BC,∠ACB=![]() ,
,
∴四边形DECF为矩形,
∴∠GDH=![]() ,
,
又∵∠MDN=![]() ,
,
∴∠GDE+∠EDH=∠HDF+∠EDH=![]() ,
,
∴∠GDE=∠HDF,
又∵∠DGE=∠DHF=![]() ,
,
∴![]() ,
,
∴ .
.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:
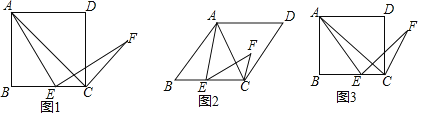
【题目】由特殊到一般、类比、转化是数学学习和研究中经常用到的思想方法.下面是对一道几何题进行变式探究的思路,请你运用上述思想方法完成探究任务.问题情境:在四边形ABCD中,AC是对角线,E为边BC上一点,连接AE.以E为旋转中心,将线段AE顺时针旋转,旋转角与∠B相等,得到线段EF,连接CF.
(1)特例如图1,若四边形ABCD是正方形,求证:AC⊥CF;
(2)拓展分析一:如图2,若四边形ABCD是菱形,探究下列问题:
①当∠B=50°时,求∠ACF的度数;
②针对图2的条件,写出一般的结论(不必证明);
(3)拓展探究二:如图3,若四边形ABCD是矩形,且BC=kAB(k>1).若前提条件不变,特例分析中得到的结论还成立吗?若成立,请证明;若不成立,修改题中的条件使结论成立(不必证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 过点
过点![]() ,
,![]() ,与
,与![]() 轴相交于点
轴相交于点![]() .
.
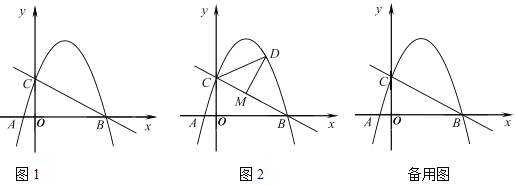
(1)求抛物线的解析式;
(2)在![]() 轴正半轴上存在点
轴正半轴上存在点![]() ,使得
,使得![]() 是等腰三角形,请求出点
是等腰三角形,请求出点![]() 的坐标;
的坐标;
(3)如图2,点![]() 是直线
是直线![]() 上方抛物线上的一个动点.过点
上方抛物线上的一个动点.过点![]() 作
作![]() 于点
于点![]() ,是否存在点
,是否存在点![]() ,使得
,使得![]() 中的某个角恰好等于
中的某个角恰好等于![]() 的2倍?若存在,请求出点
的2倍?若存在,请求出点![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点
经过点![]() .点
.点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作直线
作直线![]() 轴,点
轴,点![]() 是抛物线
是抛物线![]() 上一点,
上一点,![]() 于点
于点![]() .
.
![]() 求抛物线解析式:
求抛物线解析式:
![]() 在抛物线对称轴上是否存在一定点
在抛物线对称轴上是否存在一定点![]() ,使得
,使得![]() 永远成立?若存在,求出点
永远成立?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
![]() 若点
若点![]() 坐标为
坐标为![]() ,求
,求![]() 的最小值.
的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场要经营一种新上市的文具,进价为![]() 元
元![]() 件.试营销阶段发现:当销售单价是
件.试营销阶段发现:当销售单价是![]() 元时,每天的销售量为
元时,每天的销售量为![]() 件;销售单价每上涨
件;销售单价每上涨![]() 元,每天的销售量就减少
元,每天的销售量就减少![]() 件.
件.
(1)写出商场销售这种文具,每天所得的销售利润![]() (元)与销售单价
(元)与销售单价![]() (元)之间的函数关系式.
(元)之间的函数关系式.
(2)当销售单价定为多少元时,该文具每天的销售利润最大?最大利润为多少元?
(3)商场的营销部结合上述情况,提出了![]() ,
,![]() 两种营销方案:
两种营销方案:
方案![]() :该文具的销售单价高于进价,但不超过
:该文具的销售单价高于进价,但不超过![]() 元;
元;
方案![]() :每天销售量不少于
:每天销售量不少于![]() 件,且每件文具的利润至少为
件,且每件文具的利润至少为![]() 元.
元.
请比较哪种方案的最大利润更高,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘轮船在A处测得灯塔P在船的北偏东30°方向,轮船沿着北偏东60°方向航行16km后到达B处,这时灯塔P在船的北偏西75°方向.则灯塔P与B之间的距离等于___________km(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作,已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.
小丽:如果以10元/千克的价格销售,那么每天可售出100千克.
小强:如果以12元/千克的价格销售,那么每天可售出80千克.
小红:通过调查验证,我发现每天的销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元)之间存在一次函数关系.
(元)之间存在一次函数关系.
小强:我发现每天的销售量在70千克至100千克之间.
那么当销售单价为何值时,该超市销售这种水果每天获取的利润为320元?
查看答案和解析>>
科目:初中数学 来源: 题型:
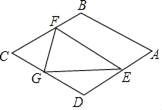
【题目】如图,在菱形ABCD中,AB=![]() ,∠B=120°,点E是AD边上的一个动点(不与A,D重合),EF∥AB交BC于点F,点G在CD上,DG=DE.若△EFG是等腰三角形,则DE的长为_____.
,∠B=120°,点E是AD边上的一个动点(不与A,D重合),EF∥AB交BC于点F,点G在CD上,DG=DE.若△EFG是等腰三角形,则DE的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com