
| A. | 0<x<1 | B. | 1<x<2 | C. | 2<x<3 | D. | 3<x<4 |
分析 结合方程的特点,可将方程的正数解看成函数y1=x2+4x+1与函数y2=$\frac{10}{x}$(x>0)的交点,画出两函数的图象,代入x=1、x=2结合函数的连贯性即可得出结论.
解答 解:方程x2+4x-$\frac{10}{x}$+1=0的正数根可看成函数y1=x2+4x+1与函数y2=$\frac{10}{x}$(x>0)的交点.
画出两函数的图象,如图所示.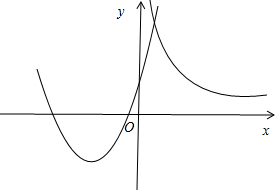
当x=1时,y1=12+4×1+1=6,y2=$\frac{10}{1}$=10,
∴此时函数y2=$\frac{10}{x}$的图象在函数y1=x2+4x+1的上方;
当x=2时,y1=22+4×2+1=13,y2=$\frac{10}{2}$=5,
∴此时函数y2=$\frac{10}{x}$的图象在函数y1=x2+4x+1的下方.
∴函数y1=x2+4x+1与函数y2=$\frac{10}{x}$(x>0)的交点的横坐标1<x<2.
故选B.
点评 本题考查了二次函数的图象以及反比例函数的图象,解题的关键是代入x=1、x=2确定交点的范围.本题属于基础题,难度不大,解决该题型题目时,根据方程的构成特点,将方程的解看成两函数图象的交点问题是关键.


 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{0.8x-200}{200}$×100%=10% | B. | $\frac{200-0.8x}{200}$×100%=10% | ||
| C. | $\frac{0.8x-200}{x}$×100%=10% | D. | $\frac{200-0.8x}{x}$×100%=10% |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | $\frac{2}{5}$ | D. | -$\frac{2}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
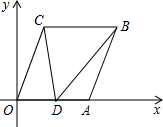 如图,在直角坐标系xOy中,已知A(6,0),B(8,6),将线段OA平移至CB,点D在x轴正半轴上(不与点A重合),连接OC,AB,CD,BD.
如图,在直角坐标系xOy中,已知A(6,0),B(8,6),将线段OA平移至CB,点D在x轴正半轴上(不与点A重合),连接OC,AB,CD,BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
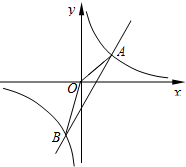 如图,已知反比例函数y1=$\frac{{k}_{1}}{x}$的图象与一次函数y2=k2x+b的图象交于A、B两点,A(2,n),B(-$\frac{1}{2}$,-2).
如图,已知反比例函数y1=$\frac{{k}_{1}}{x}$的图象与一次函数y2=k2x+b的图象交于A、B两点,A(2,n),B(-$\frac{1}{2}$,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com