
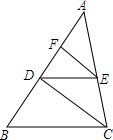
 如图,在△ABC中,EF∥DC,DE∥BC,求证:
如图,在△ABC中,EF∥DC,DE∥BC,求证:分析 (1)由平行线分线段成比例定理得出AF:FD=AE:EC,AD:DB=AE:EC,即可得出结论;
(2)由平行线得出△AFE∽△ADC,△ADE∽△ABC,得出对应边成比例,得出AF:AD=AD:AB,即可得出结论.
解答 证明:(1)∵EF∥DC,DE∥BC,
∴AF:FD=AE:EC,AD:DB=AE:EC,
∴AF:FD=AD:DB;
(2)∵EF∥DC,DE∥BC,
∴△AFE∽△ADC,△ADE∽△ABC,
∴AF:AD=AE:AC,AD:AB=AE:AC,
∴AF:AD=AD:AB,
∴AD2=AF•AB.
点评 本题考查了相似三角形的判定与性质、平行线分线段成比例定理;熟练掌握相似三角形的判定与性质、平行线分线段成比例定理,并能进行推理论证是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
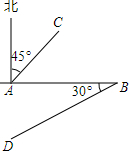 如图,是某油田的四口油井的位置图,图中1cm表示实际距离1.5km.请你仔细观察,并量一量图中的距离,用语言叙述这四口油井之间的位置关系.
如图,是某油田的四口油井的位置图,图中1cm表示实际距离1.5km.请你仔细观察,并量一量图中的距离,用语言叙述这四口油井之间的位置关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
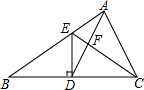 如图,在△ABC中,D是BC边上的中点,AD=AC,DE⊥BC,交AB于点E,CE与AD相交于点F,BC=10,S△CDF=6.
如图,在△ABC中,D是BC边上的中点,AD=AC,DE⊥BC,交AB于点E,CE与AD相交于点F,BC=10,S△CDF=6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
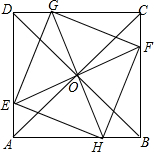 已知;如图,在正方形ABCD中,AC与BD相交于点O,EF,GH都过点O,分别交AD,BC于E,F,交CD,AB于G,H,EF⊥GH,求证:四边形EHFG是正方形.
已知;如图,在正方形ABCD中,AC与BD相交于点O,EF,GH都过点O,分别交AD,BC于E,F,交CD,AB于G,H,EF⊥GH,求证:四边形EHFG是正方形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com