Question

某市为美化市容，开展了城市绿化活动，准备种植一种新品种树苗．甲、乙两个育苗基地均已每株4元的价格出售这种树苗，并对一次性购买该种树苗不低于1000株的用户均实行优惠：甲处的优惠政策是每株树苗按原价的七五折出售；乙处的优惠政策是免收所购树苗中200株的费用，其余树苗按原价的九折出售．
（1）规定购买该种树苗只能在甲、乙两处中的一处购买，设一次性购买x（x≥1000且x为整数）株该种树苗，若在甲育苗基地购买，所花的费用为y₁元，写出y₁与x之间的函数关系式；若在乙育苗基地购买，所花的费用为y₂元，写出y₂与x之间的函数关系式（两个关系式均不要求写出自变量x的取值范围）．
（2）若在甲、乙两个育苗基地分别一次性购买1400株该种树苗，在哪处购买所花的费用较少？为什么？
（3）若在甲育苗基地以相应的优惠方式购买一批该种树苗，又在乙育苗基地以相应的优惠方式购买另一批该种树苗，两批树苗共2500株，则购买2500株该树苗所花的费用至少为多少元？这时应在甲、乙两育苗基地处分别购买该种树苗多少株？

Answer 1

解：（1）由题意得，
y₁=0.75×4x=3x，
y₂=0.9×4（x-200）=3.6x-720；

（2）应在甲处育苗基地购买所花的费用少．
当x=1400时，y₁=3×1400=4200；
y₂=3.6×1400-720=4320．
∵y₁＜y₂，
∴在甲处购买费用少；

（3）设在乙处购买a株该种树苗，则甲处购买（2500-a）株，所花钱数为W元，
∴W=3（2500-a）+3.6a-720=0.6a+6780，
∵，
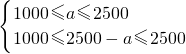
∴1000≤a≤1500，且a为整数，
∵0.6＞0，
∴W随a的增大而增大，
∴a=1000时，W_最小=7380，
∴2500-1000=1500（株）．
答：至少需要花费7380元，应在甲处购买1500株，在乙处购买1000株．
分析：（1）根据题意可得出两个关系式；
（2）把x=1400代入两个函数式计算，可得出花费少的地方；
（3）可设在乙处购买a株该种树苗，所花钱数为W元，可列出W与a的函数关系式，再根据题意列出关于a的不等式组，求a的范围，然后利用一次函数的性质进行解答．
点评：本题主要考查了一次函数的应用和不等式组的应用，解答一次函数的应用问题中，要注意自变量的取值范围必须使实际问题有意义．
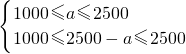