练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．一位同学做一道题：“已知两个多项式A、B，计算2A-B”．他误将“2A-B”看成“A-2B”，求得的结果为5x2-2x+4．已知B=-2x2+3x-7，求2A-B的正确答案．

    分析 根据题意确定出A，将A与B代入2A-B中，去括号合并即可得到结果．

    解答 解：根据题意得：A-2（-2x2+3x-7）=5x2-2x+4，即A=x2+4x-10，
    则2A-B=2（x2+4x-10）-（-2x2+3x-7）=2x2+8x-20+2x2-3x+7=4x2+5x-13．

    点评 此题考查了整式的加减，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    8．如图，一把矩形直尺沿直线断开并错位，点E、D、B、F在同一条直线上，若∠ADE=125°，则∠DBC的度数为55°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．面积为π的正方形的内切圆面积为$\frac{1}{4}$π2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．小青家有一块如图的四边形土地要流转出去，其中∠D=∠B=90°，∠C=135°，用激光测距仪测得：BC=$\sqrt{2}$（千米），DC=3$\sqrt{2}$（千米），求这块四边形土地的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．象棋在我国具有悠久的历史，其中马的行棋规则是“马走日”，即马每步走日字格的对角点，又称“马踩八方”，如图1中的马走一步可以有8种不同的选择，走向8个日字格的对角点．在图2中的象棋棋盘中，每个小正方形方格的边长都是1．
    （1）若图2中马必须先走到直线a上，再走到“将”的位置，（把每个棋子看作是在正方形方格顶点上的点），则马走的路径之和最短是3$\sqrt{5}$．
    （2）若图2中对马的行走路线不作限制，且使马走到“将”的位置走过的路径之和最短，共有6种不同的方法．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．某汽车厂计划半年内每月生产汽车20辆，由于另有任务，每月工作人数不一定相等，实际每月生产量与计划量相比情况如表（增加为正，减少为负）
    月份一二三四五六
    增减（辆）+3-2-1+4+2-5
    ①生产量最多的一月比生产量最少的一月多生产多少辆？
    ②半年内总产量是多少？比计划增加了还是减少了，增加或减少多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

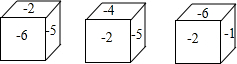    10．一个正方体的六个面上分别标有-1，-2，-3，-4，-5，-6中的一个数，各个面上所标数字都不相同，如图是这个正方体的三种放置方法，三个正方体下底面所标数字分别是a，b，c，则abc=-72．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．如图，一把直尺沿直线断开并错位，点E、D、B、F在同一条直线上，若∠ADE=120°，则∠DBC的度数为60°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．若多项式x2+x+m可以分解为（x+3）（x-2），则方程x2+x+m=0根是（　　）
    A．x=-3B．x=2C．x=-3或x=2D．无法确定

    查看答案和解析>>

    同步练习册答案