Question

11．如图，AB是⊙O的直径，AB=2，分别以A，B为圆心，1为半径画弧与⊙O交于C，E，D，F，则阴影部分的面积是$\sqrt{3}$-$\frac{π}{3}$．

Answer 1

分析 连接各半径，得△ACO是等边三角形，则扇形ACE和扇形BDF的圆心角分别为120°，半径为1；根据三角函数求三角形的高CG的长，从而可以求△ACO的面积，得出小弓形AC的面积；所以阴影部分的面积=大圆的面积-两个120°的扇形的面积-4个小弓形的面积．

解答 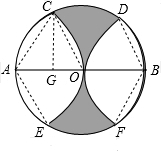解：连接AC、AE、OC、BD、BF，过C作CG⊥OA于G，
∵OC=OA=AC=1，
∴△ACO是等边三角形，
∴∠COA=∠CAO=60°，
同理∠EAO=60°，
∴∠CAE=∠DBF=120°，
在Rt△AGC中，sin∠CAO=$\frac{CG}{AC}$，
sin60°=$\frac{CG}{1}$，CG=1×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$，
∴S_弓形=S_扇形OCA-S_△ACO=$\frac{60π×{1}^{2}}{360}$-$\frac{1}{2}$×1×$\frac{\sqrt{3}}{2}$=$\frac{π}{6}$-$\frac{\sqrt{3}}{4}$，
∴S_阴影=π×1²-$\frac{240π×{1}^{2}}{360}$-4（$\frac{π}{6}$-$\frac{\sqrt{3}}{4}$）=π-$\frac{2π}{3}$-$\frac{2π}{3}$+$\sqrt{3}$=$\sqrt{3}$-$\frac{π}{3}$，
故答案为：$\sqrt{3}$-$\frac{π}{3}$．

点评 本题是圆中求阴影部分的面积，熟练掌握扇形面积的计算公式：设圆心角是n°，圆的半径为R的扇形面积为S，则 S_扇形=$\frac{nπ{R}^{2}}{360}$或S_扇形=$\frac{1}{2}$lR（其中l为扇形的弧长）；求阴影面积常用的方法：①直接用公式法； ②和差法； ③割补法；本题运用了和差法求面积．