
科目:初中数学 来源: 题型:选择题
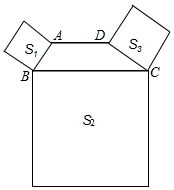 如图,四边形ABCD中,AD∥BC,∠ABC+∠DCB=90°,且BC=2AD,以AB、BC、DC为边向外作正方形,其面积分别为S1、S2、S3,若S1=3,S3=9,则S2的值为( )
如图,四边形ABCD中,AD∥BC,∠ABC+∠DCB=90°,且BC=2AD,以AB、BC、DC为边向外作正方形,其面积分别为S1、S2、S3,若S1=3,S3=9,则S2的值为( )| A. | 12 | B. | 18 | C. | 24 | D. | 48 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
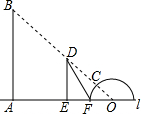 学生在操场上利用三角函数测量旗杆AB的高,直线l为水平地面,两个同学把30°的三角板和量角器按如图所示的方式垂直放在地面上,量角器的零刻度线与地面重合,此时旗杆顶部B的影子恰好落在三角形板的顶点D处和量角器37°的刻度C处,已知三角形板的边DE=60厘米,量角器的半径r=25厘米,量角器的圆心O到A的距离为5米.
学生在操场上利用三角函数测量旗杆AB的高,直线l为水平地面,两个同学把30°的三角板和量角器按如图所示的方式垂直放在地面上,量角器的零刻度线与地面重合,此时旗杆顶部B的影子恰好落在三角形板的顶点D处和量角器37°的刻度C处,已知三角形板的边DE=60厘米,量角器的半径r=25厘米,量角器的圆心O到A的距离为5米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
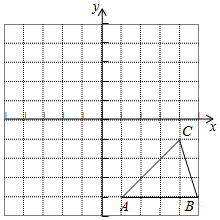 已知,方格纸中的每个小正方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
已知,方格纸中的每个小正方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
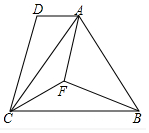 如图,在四边形ABCD中,AB=BC,BF是∠ABC的平分线,连接AB.
如图,在四边形ABCD中,AB=BC,BF是∠ABC的平分线,连接AB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com