
【题目】如图,△ABC和△ADE都是等腰三角形,且∠BAC=90°,∠DAE=90°,B,C,D在同一条直线上.求证:BD=CE.

科目:初中数学 来源: 题型:
【题目】某公司有10名工作人员,他们的月工资情况如表,
职务 | 经理 | 副经理 | A类职员 | B类职员 | C类职员 |
人数 | 1 | 2 | 2 | 4 | 1 |
月工资(万元/人) | 2 | 1.2 | 0.8 | 0.6 | 0.4 |
根据表中信息,该公司工作人员的月工资的众数是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 下列是假命题的是( )
A.对角线互相平分且相等的四边形是矩形
B.垂直于弦的直径必平分弦
C.在同圆或等圆中,相等的弦所对的圆周角相等
D.顺次连接平行四边形的四边中点,得到的四边形是平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
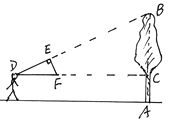
【题目】如图,小明用自制的直角三角形纸板DEF测量树AB的高度,他调整自己的位置,使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=40 cm,EF=20 cm,测得边DF离地面的高度AC=1.5 m, CD=10 m,请你帮小明求下树的高度。
查看答案和解析>>
科目:初中数学 来源: 题型:
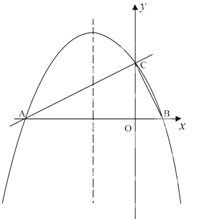
【题目】如图,在平面直角坐标系xoy中,直线![]() 与x 轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是
与x 轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是![]() 且经过A、C两点,与x轴的另一交点为点B.
且经过A、C两点,与x轴的另一交点为点B.
(1)①直接写出点B的坐标;②求抛物线解析式.
(2)若点P为直线AC上方的抛物线上的一点,连接PA,PC.求△PAC的面积的最大值,并求出此时点P的坐标.
(3)抛物线上是否存在点M,过点M作MN垂直x轴于点N,使得以点A、M、N为顶点的三角形与△ABC相似?若存在,直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件,是必然事件的是( )
A.投掷一次骰子向上一面的点数是6B.童威在罚球线上投篮一次未投中
C.任意画一个多边形其外角和是360°D.经过有交通信号灯的路口遇到红灯
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的边BC与x轴重合,连接对角线BD交y轴于点E,过点A作AG⊥BD于点G,直线GF交AD于点F,AB、OC的长分别是一元二次方程x-5x+6=0的两根(AB>OC),且tan∠ADB=![]() .
.
(1)求点E、点G的坐标;
(2)直线GF分△AGD为△AGF与△DGF两个三角形,且S△AGF:S△DGF =3:1,求直线GF的解析式;
(3)点P在y轴上,在坐标平面内是否存在一点Q,使以点B、D、P、Q为顶点的四边形是矩形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
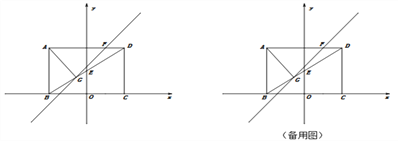
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com