
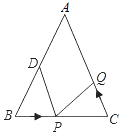
【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.
(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?
【答案】(1)利用SAS公式求证(2)![]()
【解析】
解:(1)①∵![]() 秒,
秒,
∴![]() 厘米,
厘米,
∵![]() 厘米,点
厘米,点![]() 为
为![]() 的中点,
的中点,
∴![]() 厘米.
厘米.
又∵![]() 厘米,
厘米,
∴![]() 厘米,
厘米,
∴![]() .
.
又∵![]() ,
,
∴![]() ,
,
∴![]() .
.
②∵![]() , ∴
, ∴![]() ,
,
又∵![]() ,
,![]() ,则
,则![]() ,
,
∴点![]() ,点
,点![]() 运动的时间
运动的时间![]() 秒,
秒,
∴![]() 厘米/秒.
厘米/秒.
(2)设经过![]() 秒后点
秒后点![]() 与点
与点![]() 第一次相遇,
第一次相遇,
由题意,得![]() ,
,
解得![]() 秒.
秒.
∴点![]() 共运动了
共运动了![]() 厘米.
厘米.
∵![]() ,
,
∴点![]() 、点
、点![]() 在
在![]() 边上相遇,
边上相遇,
∴经过![]() 秒点
秒点![]() 与点
与点![]() 第一次在边
第一次在边![]() 上相遇.
上相遇.
(1)①根据时间和速度分别求得两个三角形中的边的长,根据SAS判定两个三角形全等.
②根据全等三角形应满足的条件探求边之间的关系,再根据路程=速度×时间公式,先求得点P运动的时间,再求得点Q的运动速度;
(2)根据题意结合图形分析发现:由于点Q的速度快,且在点P的前边,所以要想第一次相遇,则应该比点P多走三角形的两个边AB,AC的长.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】密苏里州圣路易斯拱门是座雄伟壮观的抛物线形的建筑物,是美国最高的独自挺立的纪念碑,如图.拱门的地面宽度为200米,两侧距地面高150米处各有一个观光窗,两窗的水平距离为100米,求拱门的最大高度. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:

(1)小明总共剪开了_______条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,B、C、D三点在同一条直线上,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )

A. ∠A与∠D互为余角 B. ∠A=∠2 C. △ABC≌△ CED D. ∠1=∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
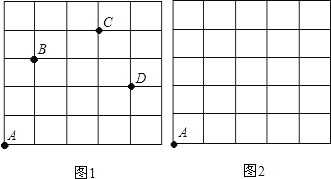
【题目】如图,一只甲虫在5![]() 5的方格(每一格边长为1)上沿着网格线运动,从A处出发去看望B、C、D处的甲虫,规定:向上向右为正,向下向左为负.例如:从A到B记为:
5的方格(每一格边长为1)上沿着网格线运动,从A处出发去看望B、C、D处的甲虫,规定:向上向右为正,向下向左为负.例如:从A到B记为:![]() (+1,+3);从C到D 记为:
(+1,+3);从C到D 记为:![]() (+1,-2),其中第一个数表示左右方向,第二个数表示上下方向.
(+1,-2),其中第一个数表示左右方向,第二个数表示上下方向.
(1)填空:![]() 记为( , ),
记为( , ), ![]() 记为( , );
记为( , );
(2)若甲虫的行走路线为:![]() ,请你计算甲虫走过的路程.
,请你计算甲虫走过的路程.
(3)若这只甲虫去Q的行走路线依次为:A→M(+2,+2),M→N(+2,-1),N→P(-2,+3),P→Q(-1,-2),请依次在图2标出点M、N、P、Q的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y是x的二次函数,当x=2时,y=﹣4,当y=4时,x恰为方程2x2﹣x﹣8=0的根.
(1)解方程 2x2﹣x﹣8=0
(2)求这个二次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,∠ABC=2∠C,BE平分∠ABC交AC于E,AD⊥BE于D,下列结论:①AC﹣BE=AE;②点E在线段BC的垂直平分线上;③∠DAE=∠C;④BC=4AD,其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com