
【题目】如图,已知正方形ABCD,从顶点A引两条射线分别交BC,CD于点E,F,且∠EAF=45°.
求证:BE+DF=EF.

【答案】证明见解析
【解析】
延长CD到G,使DG=BE,利用“边角边”证明△ABE和△ADG全等,根据全等三角形对应边相等可得AG=AE,全等三角形对应角相等可得∠DAG=∠BAE,然后求出∠EAF=∠GAF,再利用“边角边”证明△AEF和△AGF全等,根据全等三角形对应边相等可得EF=GF,然后结合图形整理即可得证.
证明:延长CD到点G,使DG=BE,连接AG.
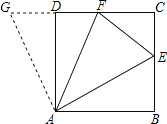
在正方形ABCD中,AB=AD,∠B=∠ADC=90°,
所以∠ADG=∠B.
在△ABE和△ADG中,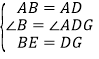 ,
,
所以△ABE≌△ADG(SAS).
所以AE=AG,∠BAE=∠DAG.
因为∠EAF=45°,
所以∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=90°-45°=45°.
所以∠EAF=∠GAF,
在△AEF和△AGF中,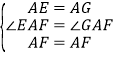 ,
,
所以△AEF≌△AGF(SAS).
所以EF=GF.
所以EF=GF=DG+DF=BE+DF,
即BE+DF=EF.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】【定义】已知P为△ABC所在平面内一点,连接PA,PB,PC,在△PAB,△PBC和△PAC中,若存在一个三角形与△ABC相似(全等除外),那么就称P为△ABC的“共相似点”,根据“共相似点”是否落在三角形的内部,边上或外部,可将其分为“内共相似点”,“边共相似点”或“外共相似点”.
(1)据定义可知,等边三角形(填“存在”或“不存在”)共相似点.
(2)如图1,若△ABC的一个边共相似点P与其对角顶点B的连线,将△ABC分割成的两个三角形恰与原三角形均相似,试判断△ABC的形状,并说明理由.
(3)如图2,在△ABC中,∠A<∠B<∠C,高线CD与角平分线BE交于点P,若P是△ABC的一个内共相似点,试说明点E是△ABC的边共相似点,并直接写出∠A的度数.
(4)如图3,在Rt△ABC中,∠C=90°,∠A=30°,BC= ![]() ,若△PBC与△ABC相似,则满足条件的P点共有个,顺次连接所有满足条件的P点而围成的多边形的周长为 .
,若△PBC与△ABC相似,则满足条件的P点共有个,顺次连接所有满足条件的P点而围成的多边形的周长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:ABCD的两边AB,AD的长是关于x的方程x2﹣mx+ ![]() ﹣
﹣ ![]() 的两个实数根.
的两个实数根.
(1)当m为何值时,ABCD是菱形?
(2)若AB的长为2,那么ABCD的周长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地开辟一块长方形的荒地用于新建一个以环保为主题的公园.已知这块荒地的长是宽的2倍,它的面积为400 000 m2,那么:
(1)荒地的宽是多少?有1 000 m吗?(结果保留一位小数)
(2)如果要求结果保留整数,那么宽大约是多少?
(3)计划在该公园中心建一个圆形花圃,面积是800 m2,你能估计它的半径吗?(要求结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;
(1)若B、C在DE的同侧(如图所示)且AD=CE.求证:AB⊥AC;
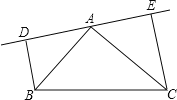
(2)若B、C在DE的两侧(如图所示),其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠C=90° 
(1)利用尺规作∠B 的角平分线交AC于D,以BD为直径作⊙O交AB于E(保留作图痕迹,不写作法);
(2)综合应用:在(1)的条件下,连接DE ①求证:CD=DE;
②若sinA= ![]() ,AC=6,求AD.
,AC=6,求AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自动化车间计划生产480个零件,当生产任务完成一半时,停止生产进行自动化程序软件升级,用时20分钟,恢复生产后工作效率比原来提高了![]() ,结果完成任务时比原计划提前了40分钟,求软件升级后每小时生产多少个零件?
,结果完成任务时比原计划提前了40分钟,求软件升级后每小时生产多少个零件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com