
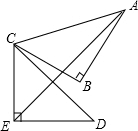
 如图,在Rt△ABC中,∠B=90°,AB=BC=2,将△ABC绕点C顺时针旋转60°,得到△DEC,则AE的长是$\sqrt{2}$+$\sqrt{6}$.
如图,在Rt△ABC中,∠B=90°,AB=BC=2,将△ABC绕点C顺时针旋转60°,得到△DEC,则AE的长是$\sqrt{2}$+$\sqrt{6}$. 分析 如图,连接AD,由题意得:CA=CD,∠ACD=60°,得到△ACD为等边三角形根据AC=AD,CE=ED,得出AE垂直平分DC,于是求出EO=$\frac{1}{2}$DC=$\sqrt{2}$,OA=AC•sin60°=$\sqrt{6}$,最终得到答案AE=EO+OA=$\sqrt{2}$+$\sqrt{6}$.
解答  解:如图,连接AD,
解:如图,连接AD,
由题意得:CA=CD,∠ACD=60°,
∴△ACD为等边三角形,
∴AD=CA,∠DAC=∠DCA=∠ADC=60°;
∵∠ABC=90°,AB=BC=2,
∴AC=AD=2$\sqrt{2}$,
∵AC=AD,CE=ED,
∴AE垂直平分DC,
∴EO=$\frac{1}{2}$DC=$\sqrt{2}$,OA=CA•sin60°=$\sqrt{6}$,
∴AE=EO+OA=$\sqrt{2}$+$\sqrt{6}$,
故答案为$\sqrt{2}$+$\sqrt{6}$.
点评 本题考查了图形的变换-旋转,等腰直角三角形的性质,等边三角形的判定和性质,线段的垂直平分线的性质,准确把握旋转的性质是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{{x}_{1}+{x}_{2}+{x}_{3}}{3}$ | B. | $\frac{a{x}_{1}+b{x}_{2}+c{x}_{3}}{a+b+c}$ | ||
| C. | $\frac{a{x}_{1}+b{x}_{2}+c{x}_{3}}{3}$ | D. | $\frac{a+b+c}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,E为?ABCD的边AB延长线上的一点,且BE:AB=2:3,△BEF的面积为4,则?ABCD的面积为( )
如图,E为?ABCD的边AB延长线上的一点,且BE:AB=2:3,△BEF的面积为4,则?ABCD的面积为( )| A. | 30 | B. | 27 | C. | 14 | D. | 32 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届湖北省九年级三月月考数学试卷(解析版) 题型:判断题
已知,A,B 两市相距 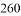 千米,甲车从 A 市前往 B 市运送物资,行驶
千米,甲车从 A 市前往 B 市运送物资,行驶  小时在 M 地汽车出现故障,立即通知技术人员乘乙车从 A 市赶来维修(通知时间忽略不计),乙车到达 M 地后又经过
小时在 M 地汽车出现故障,立即通知技术人员乘乙车从 A 市赶来维修(通知时间忽略不计),乙车到达 M 地后又经过  分钟修好甲车后以原速原路返回,同时甲车以原速
分钟修好甲车后以原速原路返回,同时甲车以原速 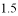 倍的速度前往 B 市,如图是两车距 A 市的路程
倍的速度前往 B 市,如图是两车距 A 市的路程  (千米)与甲车行驶时间
(千米)与甲车行驶时间  (小时)之间的函数图象,结合图象回答下列问题:
(小时)之间的函数图象,结合图象回答下列问题:
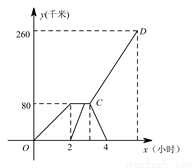
(1)直接写出甲车提速后的速度、乙车的速度、点  的坐标;
的坐标;
(2)求乙车返回时  与
与  的函数关系式并直接写出自变量
的函数关系式并直接写出自变量  的取值范围;
的取值范围;
(3)求甲车到达 B 市时乙车已返回 A 市多长时间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com