
【题目】在平面直角坐标系 xOy中,对于点P(x,y),以及两个无公共点的图形W1和W2 , 若在图形W1和W2上分别存在点M (x1 , y1 )和N (x2 , y2 ),使得P是线段MN的中点,则称点M 和N被点P“关联”,并称点P为图形W1和W2的一个“中位点”,此时P,M,N三个点的坐标满足x= ![]() ,y=
,y= ![]()
(1)已知点A(0,1),B(4,1),C(3,﹣1),D(3,﹣2),连接AB,CD.
①对于线段AB和线段CD,若点A和C被点P“关联”,则点P的坐标为;
②线段AB和线段CD的一“中位点”是Q (2,﹣ ![]() ),求这两条线段上被点Q“关联”的两个点的坐标;
),求这两条线段上被点Q“关联”的两个点的坐标;
(2)如图1,已知点R(﹣2,0)和抛物线W1:y=x2﹣2x,对于抛物线W1上的每一个点M,在抛物线W2上都存在点N,使得点N和M 被点R“关联”,请在图1 中画出符合条件的抛物线W2;
(3)正方形EFGH的顶点分别是E(﹣4,1),F(﹣4,﹣1),G(﹣2,﹣1),H(﹣2,1),⊙T的圆心为T(3,0),半径为1.请在图2中画出由正方形EFGH和⊙T的所有“中位点”组成的图形(若涉及平面中某个区域时可以用阴影表示),并直接写出该图形的面积.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,为了估算河的宽度,我们可以在河对岸选定一个目标点P , 在近岸取点Q和S , 使点P、Q、S共线且直线PS与河垂直,接着再过点S且与PS垂直的直线a上选择适当的点T , 确定PT与过点Q且垂直PS的直线b的交点R . 如果测得QS=45m , ST=90m , QR=60m , 求河的宽度PQ . 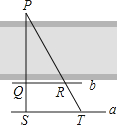
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx-5的图象经过点A(2,-1).
(1)求k的值;
(2)画出这个函数的图象;
(3)若将此函数的图象向上平移m个单位后与坐标轴围成的三角形的面积为1,请直接写出m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,反比例函数y1= ![]() 的图象与一次函数y2=ax+b的图象交于点A(1,3)和B(﹣3,m).
的图象与一次函数y2=ax+b的图象交于点A(1,3)和B(﹣3,m).
(1)求反比例函数y1= ![]() 和一次函数y2=ax+b的表达式;
和一次函数y2=ax+b的表达式;
(2)点C 是坐标平面内一点,BC∥x 轴,AD⊥BC 交直线BC 于点D,连接AC.若AC= ![]() CD,求点C的坐标.
CD,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,反比例函数y1= ![]() 的图象与一次函数y2=ax+b的图象交于点A(1,3)和B(﹣3,m).
的图象与一次函数y2=ax+b的图象交于点A(1,3)和B(﹣3,m).
(1)求反比例函数y1= ![]() 和一次函数y2=ax+b的表达式;
和一次函数y2=ax+b的表达式;
(2)点C 是坐标平面内一点,BC∥x 轴,AD⊥BC 交直线BC 于点D,连接AC.若AC= ![]() CD,求点C的坐标.
CD,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在五边形ABCDE中,∠B=90°,AB=BC=CD=1,AB∥CD,M是CD边的中点,点P由点A出发,按A→B→C→M的顺序运动.设点P经过的路程x为自变量,△APM的面积为y,则函数y的大致图象是( )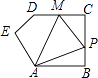
A.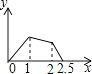
B.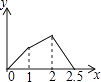
C.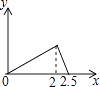
D.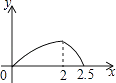
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( ) 
A.该村人均耕地面积随总人口的增多而增多
B.当该村总人口为50人时,人均耕地面积为1公顷
C.若该村人均耕地面积为2公顷,则总人口有100人
D.该村人均耕地面积y与总人口x成正比例
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com