
【题目】某学校以随机抽样的方式开展了中学生喜欢数学的程度的问卷调查,调查的结果分为A(不喜欢)、B(一般)、C(比较喜欢)、D(非常喜欢)四个等级,图1、图2是根据采集的数据绘制的两幅不完整的统计图.
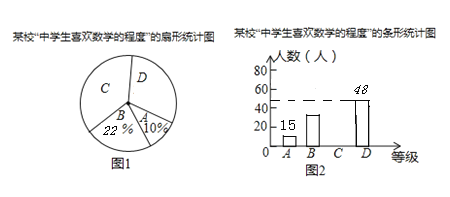
(1)本次抽样调查的样本容量是;
(2)请直接在图2中补全C对应的条形统计图;
(3)若该校有学生1000人,请根据调查结果,估计“比较喜欢”的学生人数为多少人.
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】下面是小明主设计的“作一个含30°角的直角三角形”的尺规作图过程.
已知:直线l.
![]()
求作:△ABC,使得∠ACB=90°,∠ABC=30°.
作法:如图,
![]()
①在直线l上任取两点O,A;
②以点O为圆心,OA长为半径画弧,交直线l于点B;
③以点A为圆心,AO长为半径画弧,交![]() 于点C;
于点C;
④连接AC,BC.
所以△ABC就是所求作的三角形.
根据小明设计的尺规作图过程:
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:在⊙O中,AB为直径,
∴∠ACB=90°(① ),(填推理的依据)
连接OC
∵OA=OC=AC,
∴∠CAB=60°,
∴∠ABC=30°(② ),(填推理的依据)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名大学毕业生利用“互联网+”自主创业,销售一种产品,这种产品的成本价为80元/件,经市场调查发现,该产品的日销售量![]() (单位:件)与销售单价
(单位:件)与销售单价![]() (单位:元/件)之间满足一次函数关系,如图所示.
(单位:元/件)之间满足一次函数关系,如图所示.
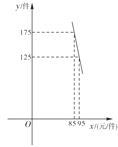
(1)求![]() 与
与![]() 之间的函数解析式,并写出自变量
之间的函数解析式,并写出自变量![]() 的取值范围;
的取值范围;
(2)求每天的销售利润![]() (单位:元)与销售单价
(单位:元)与销售单价![]() 之间的函数关系式,并求出每件销售单价为多少元时,每天的销售利润最大?最大利润是多少?
之间的函数关系式,并求出每件销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)这名大学生计划开展科技创新,以降低该产品的成本,预计在今后的销售中,日销售量与销售单价仍存在(1)中的关系.若想实现销售单价为90元时,日销售利润不低于3750元的销售目标,该产品的成本单价应不超过多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数 y=![]() 的图像经过点A(-1,a),过点A作AB⊥x轴,垂足为点B,△AOB的面积为
的图像经过点A(-1,a),过点A作AB⊥x轴,垂足为点B,△AOB的面积为![]() .
.
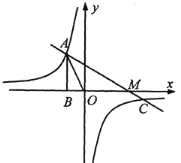
(1)求a、k的值;
(2)若一次函数y=mx+n图像经过点A和反比例函数图像上另一点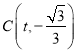 ,且与x轴交于M点,求AM的值:
,且与x轴交于M点,求AM的值:
(3)在(2)的条件下,如果以线段AM为一边作等边△AMN,顶点N在一次数函数y=bx上,则b= ______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.《九章算术》中记载:“今有甲乙二人持钱不知其数.甲得乙半而钱五十,乙得甲太半而钱亦五十.问甲、乙持钱各几何?”
译文:“假设有甲乙二人,不知其钱包里有多少钱.若乙把自己一半的钱给甲,则甲的钱数为50;而甲把自己![]() 的钱给乙,则乙的钱数也能为50.问甲、乙各有多少钱?”
的钱给乙,则乙的钱数也能为50.问甲、乙各有多少钱?”
设甲持钱为x,乙持钱为y,可列方程组为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
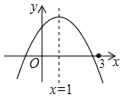
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①abc>0;②2a+b=0;③若m为任意实数,则a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2.其中,正确结论的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店销售甲、乙两种圆规,当销售5只甲种、1只乙种圆规,可获利润25元,销售6只甲种、3只乙种圆规,可获利润39元.
(1)问该文具店销售甲、乙两种圆规,每只的利润分别是多少元?
(2)在(1)中,文具店共销售甲、乙两种圆规50只,其中甲种圆规为a只,求文具店所获得利润P与a的函数关系式,并求当a≥30时P的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com