
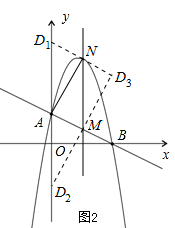
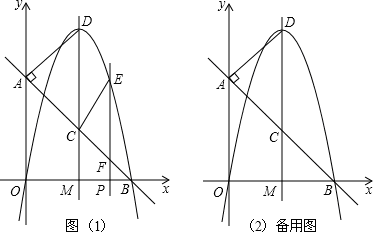
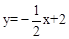 分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.
分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.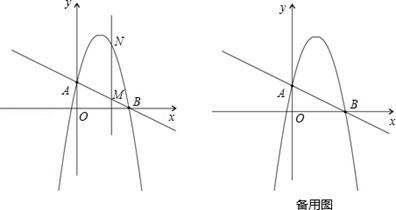
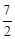 x+2(2)当t=2时,MN有最大值4(3)D点坐标为(0,6),(0,﹣2)或(4,4)
x+2(2)当t=2时,MN有最大值4(3)D点坐标为(0,6),(0,﹣2)或(4,4)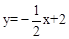 分别交y轴、x轴于A、B两点,
分别交y轴、x轴于A、B两点,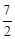 。
。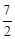 x+2。
x+2。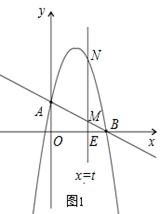
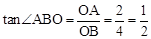 ,
,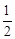 =2﹣
=2﹣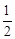 t。
t。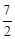 t+2。
t+2。 。
。
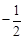 x+6;
x+6;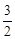 x﹣2。
x﹣2。

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 每亩树苗的收益)
每亩树苗的收益) ,
, )
)查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 经过点O、A、B三点,且A点坐标为(4,0),B的坐标为(m,
经过点O、A、B三点,且A点坐标为(4,0),B的坐标为(m, ),点C是抛物线在第三象限的一点,且横坐标为-2.
),点C是抛物线在第三象限的一点,且横坐标为-2.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的图象经过
的图象经过 和
和 两点,且交
两点,且交 轴于点
轴于点 .
. 、
、 的值;
的值; 作
作 轴交抛物线于点
轴交抛物线于点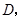 点
点 为此抛物线的顶点,试确定
为此抛物线的顶点,试确定 的形状.
的形状.

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 (a≠0)于x轴有一个交点的横坐标x的范围是( )
(a≠0)于x轴有一个交点的横坐标x的范围是( ) | x | 3.23 | 3.24 | 3.25 | 3.26 |
| y | ﹣0.06 | ﹣0.02 | 0.03 | 0.09 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com