
【题目】如图,一个三角形的纸片ABC,其中∠A=∠C.
(1)把△ABC纸片按(如图1)所示折叠,使点A落在BC边上的点F处,DE是折痕,说明BC∥DF;
(2)把△ABC纸片沿DE折叠,当点A落在四边形BCED内时 (如图2),探索∠C与∠1+∠2之间的大小关系,并说明理由;
(3)当点A落在四边形BCED外时(如图3),∠C与∠1、∠2的关系是(直接写出结论)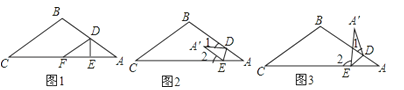
【答案】解:(1)根据折叠的性质得:∠DFE=∠A,
∵∠A=∠C,
∴∠DFE=∠C,
∴BC∥DF;
(2)2∠C=∠1+∠2,
理由:∵四边形的内角和等于360°,
∴∠A+∠A′+∠ADA′+∠AEA′=360°.
又∵∠1+∠ADA′+∠2+∠AEA′=360°,
∴∠A+∠A′=∠1+∠2.
又∵∠A=∠A′,
∴2∠A=∠1+∠2,
∵∠A=∠C,
∴2∠C=∠1+∠2;
(3)∠2﹣∠1=2∠C,
证明如下:由题意得:∠A′ED=∠AED(设为α),∠A′DE=∠ADE(设为β);
∵∠2+2α=180°,∠1=β﹣∠BDE
=β﹣(∠A+α),
∴∠2﹣∠1
=180°﹣(α+β)+∠A;
∵∠A=180°﹣(α+β),
∴∠2﹣∠1=2∠A,
∵∠A=∠C,
∴2∠C=∠2﹣∠1.
故答案为:2∠C=∠2﹣∠1.
【解析】(1)根据折叠的性质得∠DFE=∠A,由已知得∠A=∠C,于是得到∠DFE=∠C,即可得到结论;
(2)先根据四边形的内角和等于360°得出∠A+∠A′=∠1+∠2,再由图形翻折变换的性质即可得出结论;
(3)∠A′ED=∠AED(设为α),∠A′DE=∠ADE(设为β),于是得到∠2+2α=180°,∠1=β﹣∠BDE=β﹣(∠A+α),推出∠2﹣∠1=180°﹣(α+β)+∠A,根据三角形的内角和得到∠A=180°﹣(α+β),证得∠2﹣∠1=2∠A,于是得到结论.
【考点精析】解答此题的关键在于理解三角形的内角和外角的相关知识,掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角,以及对三角形的外角的理解,了解三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】下列命题中,其中正确命题的个数为( )个.
①方差是衡量一组数据波动大小的统计量;②影响超市进货决策的主要统计量是众数;③折线统计图反映一组数据的变化趋势;④水中捞月是必然事件.
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】刘翔在出征雅典奥运会前刻苦进行110米跨栏训练,教练对他10次的训练成绩进行分析,判断他的成绩是否稳定,则教练需要知识刘翔这10次成绩的( ).
A. 众数 B. 方差 C. 平均数 D. 频数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长为6,∠ABC,∠ACB的角平分线交于点D,过点D作EF∥BC,交AB、CD于点E、F,则EF的长度为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系内,把抛物线y=(x﹣1)2+3向下平移2个单位,那么所得抛物线的解析式是( )
A.y=(x﹣3)2
B.y=(x+1)2
C.y=(x﹣1)2+5
D.y=(x﹣1)2+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①满足a+b>c的a,b,c三条线段一定能组成三角形;②三角形的三条高交于三角形内一点;③三角形的外角大于它的任何一个内角.其中错误的有( )
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com