
°ĺŐ‚ńŅ°Ņ◊ŘļŌŐ‚°£
£®1£©‘ń∂Ń“‘Ō¬ńŕ»›≤ĘĽōīūő Ő‚£ļ
–°Ų©”√’‚łŲ∑Ĺ∑®ĹÝ––Ńň≥Ę ‘£¨Ķ„ ![]() ŌÚ…Ō∆Ĺ“∆3łŲĶ•őĽļůĶń∂‘”¶Ķ„
ŌÚ…Ō∆Ĺ“∆3łŲĶ•őĽļůĶń∂‘”¶Ķ„ ![]() Ķń◊ÝĪÍő™ £¨ ĻżĶ„
Ķń◊ÝĪÍő™ £¨ ĻżĶ„ ![]() Ķń÷ĪŌŖĶńĹ‚őŲ Ĺő™.
Ķń÷ĪŌŖĶńĹ‚őŲ Ĺő™.
£®2£©–°Ų©◊‘ľļ”÷ŐŠ≥ŲŃň“ĽłŲ–¬ő Ő‚«Ž»ęįŗÕ¨—ß“Ľ∆ūĹ‚īūļÕľž—ťīň∑Ĺ∑®£¨«Žń„“≤ ‘ ‘Ņī£ļĹę÷ĪŌŖ ![]() ŌÚ”“∆Ĺ“∆1łŲĶ•őĽ£¨∆Ĺ“∆ļů÷ĪŌŖĶńĹ‚őŲ Ĺő™ £¨ ŃŪÕ‚÷ĪĹ”Ĺę÷ĪŌŖ
ŌÚ”“∆Ĺ“∆1łŲĶ•őĽ£¨∆Ĺ“∆ļů÷ĪŌŖĶńĹ‚őŲ Ĺő™ £¨ ŃŪÕ‚÷ĪĹ”Ĺę÷ĪŌŖ ![]() ŌÚ£®ŐÓ°į…Ō°ĪĽÚ°įŌ¬°Ī£©∆Ĺ“∆łŲĶ•őĽ“≤ń‹Ķ√ĶĹ’‚Őű÷ĪŌŖ.
ŌÚ£®ŐÓ°į…Ō°ĪĽÚ°įŌ¬°Ī£©∆Ĺ“∆łŲĶ•őĽ“≤ń‹Ķ√ĶĹ’‚Őű÷ĪŌŖ.
£®3£©«Žń„ľŐ–ÝņŻ”√’‚łŲ∑Ĺ∑®Ĺ‚ĺŲő Ő‚£ļ
∂‘”ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶxOyńŕĶńÕľ–őM£¨ĹęÕľ–őM…Ōňý”–Ķ„∂ľŌÚ…Ō∆Ĺ“∆3łŲĶ•őĽ£¨‘ŔŌÚ”“∆Ĺ“∆1łŲĶ•őĽ£¨ő“√«į—’‚łŲĻż≥Ő≥∆ő™Õľ–őMĶń“Ľīő°į–Ī∆Ĺ“∆°Ī. «ůĹę÷ĪŌŖ ![]() ĹÝ––ŃĹīő°į–Ī∆Ĺ“∆°ĪļůĶ√ĶĹĶń÷ĪŌŖĶńĹ‚őŲ Ĺ.
ĹÝ––ŃĹīő°į–Ī∆Ĺ“∆°ĪļůĶ√ĶĹĶń÷ĪŌŖĶńĹ‚őŲ Ĺ.
°ĺīūįł°Ņ
£®1£©![]() £Ľ
£Ľ![]()
£®2£©![]() £Ľ…Ō£Ľ2
£Ľ…Ō£Ľ2
£®3£©
Ĺ‚£ļ÷ĪŌŖ ![]() …ŌĶńĶ„
…ŌĶńĶ„ ![]() ĹÝ––“Ľīő°į–Ī∆Ĺ“∆°ĪļůĶń∂‘”¶Ķ„Ķń◊ÝĪÍő™
ĹÝ––“Ľīő°į–Ī∆Ĺ“∆°ĪļůĶń∂‘”¶Ķ„Ķń◊ÝĪÍő™ ![]() £¨ĹÝ––ŃĹīő°į–Ī∆Ĺ“∆°ĪļůĶń∂‘”¶Ķ„Ķń◊ÝĪÍő™
£¨ĹÝ––ŃĹīő°į–Ī∆Ĺ“∆°ĪļůĶń∂‘”¶Ķ„Ķń◊ÝĪÍő™ ![]() £ģ
£ģ
…Ťĺ≠ĻżŃĹīő°į–Ī∆Ĺ“∆°ĪļůĶ√ĶĹĶń÷ĪŌŖĶńĹ‚őŲ Ĺő™ ![]() £ģ
£ģ
Ĺę ![]() Ķ„Ķń◊ÝĪÍīķ»Ž£¨Ķ√
Ķ„Ķń◊ÝĪÍīķ»Ž£¨Ķ√ ![]() £ģ
£ģ
Ĺ‚Ķ√ ![]() £ģ
£ģ
ňý“‘ŃĹīő°į–Ī∆Ĺ“∆°ĪļůĶ√ĶĹĶń÷ĪŌŖĶńĹ‚őŲ Ĺő™ ![]()
°ĺĹ‚őŲ°Ņ£®1£©łýĺ›∆Ĺ“∆Ķń–‘÷ £¨ŌÚ”“∆Ĺ“∆Ńň3łŲĶ•őĽĶ√ĶĹA °š£®1,1£©£¨÷ĪŌŖĹ‚őŲ Ĺłýĺ›…Ōľ”Ō¬ľűĶ√ĶĹy=-2x+3.
£®2£©÷ĪŌŖĹ‚őŲ Ĺłýĺ›◊ůľ””“ľűĶ√ĶĹy=-2x+2.łýĺ›∆Ĺ“∆Ķń–‘÷ Ķ√ĶĹŌÚ…Ō∆Ĺ“∆2łŲĶ•őĽ.
£®3£©łýĺ›°į–Ī∆Ĺ“∆°ĪĶń∂®“ŚĶ√≥ŲĶ„◊ÝĪÍ£®3,4£©£¨ĹęĶ„īķ»Ž÷ĪŌŖĹ‚őŲ Ĺ«ů≥Ų÷ĪŌŖĹ‚őŲ ĹľīŅ….


 Ņŕň„ń‹ ÷ŌĶŃ–īūįł
Ņŕň„ń‹ ÷ŌĶŃ–īūįł
| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņľ∆ň„Ő‚
£®1£©ľ∆ň„£ļ ![]()
£®2£©£®©Āa2£©3©Ā£®©Āa3£©2+2a5£®©Āa£©
£®3£©(2a+b)(2a£≠b)+3(2a£≠b) 2+(£≠3a)(4a£≠3b)
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨
‘ŕ”…ĪŖ≥§∂ľő™1łŲĶ•őĽ≥§∂»Ķń–°’ż∑Ĺ–ő◊ť≥…Ķń ![]() ’ż∑Ĺ–őÕÝłŮ÷–£¨Ķ„A £¨ B £¨ P ∂ľ‘ŕłŮĶ„…Ō£ģ«ŽĽ≠≥Ų“‘ABő™ĪŖĶńłŮĶ„ňńĪŖ–ő£®ňńłŲ∂•Ķ„∂ľ‘ŕłŮĶ„ĶńňńĪŖ–ő£©£¨“™«ůÕ¨ Ī¬ķ◊„“‘Ō¬ŐűľĢ£ļ
’ż∑Ĺ–őÕÝłŮ÷–£¨Ķ„A £¨ B £¨ P ∂ľ‘ŕłŮĶ„…Ō£ģ«ŽĽ≠≥Ų“‘ABő™ĪŖĶńłŮĶ„ňńĪŖ–ő£®ňńłŲ∂•Ķ„∂ľ‘ŕłŮĶ„ĶńňńĪŖ–ő£©£¨“™«ůÕ¨ Ī¬ķ◊„“‘Ō¬ŐűľĢ£ļ
ŐűľĢ1£ļĶ„PĶĹňńĪŖ–őĶńŃĹłŲ∂•Ķ„ĶńĺŗņŽŌŗĶ»£Ľ
ŐűľĢ2£ļĶ„P‘ŕňńĪŖ–őĶńńŕ≤ŅĽÚ∆šĪŖ…Ō£Ľ
ŐűľĢ3£ļňńĪŖ–ő÷Ń…Ŕ“Ľ◊ť∂‘ĪŖ∆Ĺ––£ģ
£®1£©‘ŕÕľĘŔ÷–Ľ≠≥Ų∑ŻļŌŐűľĢĶń“ĽłŲ ![]() ABCD £¨ ĻĶ„P‘ŕňýĽ≠ňńĪŖ–őĶńńŕ≤Ņ£Ľ
ABCD £¨ ĻĶ„P‘ŕňýĽ≠ňńĪŖ–őĶńńŕ≤Ņ£Ľ
£®2£©‘ŕÕľĘŕ÷–Ľ≠≥Ų∑ŻļŌŐűľĢĶń“ĽłŲňńĪŖ–őABCD £¨ ĻĶ„P‘ŕňýĽ≠ňńĪŖ–őĶńĪŖ…Ō£Ľ
£®3£©‘ŕÕľĘŘ÷–Ľ≠≥Ų∑ŻļŌŐűľĢĶń“ĽłŲňńĪŖ–őABCD £¨ Ļ°ŌD=90°„£¨«“°ŌA°Ŕ90°„£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨“—÷™Ň◊őÔŌŖy1=-x2+4xļÕ÷ĪŌŖy2=2x£ģő“√«‘ľ∂®£ļĶĪx»ő»°“Ľ÷Ķ Ī£¨x∂‘”¶ĶńļĮ ż÷Ķ∑÷Īūő™y1°Ęy2£¨»Űy1=y2£¨ľ«M=y1=y2£¨Ō¬Ń–Ň–∂Ō£ļĘŔĶĪx£ĺ2 Ī£¨M=y2£ĽĘŕĶĪx£ľ0 Ī£¨x÷Ķ‘Ĺīů£¨M÷Ķ‘Ĺīů£ĽĘŘ ĻĶ√Mīů”ŕ4Ķńx÷Ķ≤Ľīś‘ŕ£ĽĘ‹»ŰM=2£¨‘Úx=1£ģ∆š÷–’ż»∑Ķń”–£®°°°°£©
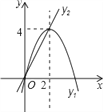
A. ĘŘĘ‹ B. ĘŕĘŘ C. ĘŕĘ‹ D. ĘŔĘ‹
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨Ň◊őÔŌŖy=ax2+bx+c£®a°Ŕ0£©”Žy÷ŠĹĽ”ŕĶ„C£®0£¨4£©£¨”Žx÷ŠĹĽ”ŕĶ„AļÕĶ„B£¨∆š÷–Ķ„AĶń◊ÝĪÍő™£®2£¨0£©£¨Ň◊őÔŌŖĶń∂‘≥∆÷Šx=-1”ŽŇ◊őÔŌŖĹĽ”ŕĶ„D£¨”Ž÷ĪŌŖBCĹĽ”ŕĶ„E£ģ

£®1£©«ůŇ◊őÔŌŖĶńĹ‚őŲ Ĺ£Ľ
£®2£©»ŰĶ„F «÷ĪŌŖBC…Ō∑ĹĶńŇ◊őÔŌŖ…ŌĶń“ĽłŲ∂ĮĶ„£¨ «∑Ůīś‘ŕĶ„F ĻňńĪŖ–őBOCFĶń√śĽż◊Óīů£¨»Űīś‘ŕ£¨«ů≥ŲĶ„FĶń◊ÝĪÍ£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”…£Ľ
£®3£©∆Ĺ––”ŕDEĶń“ĽŐű∂Į÷ĪŌŖl”Ž÷ĪŌŖBCŌŗĹĽ”ŕĶ„P£¨”ŽŇ◊őÔŌŖŌŗĹĽ”ŕĶ„Q£¨»Ű“‘D°ĘE°ĘP°ĘQő™∂•Ķ„ĶńňńĪŖ–ő «∆Ĺ––ňńĪŖ–ő£¨«ůĶ„PĶń◊ÝĪÍ£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°ŅĪĪĺ©Ķ»5łŲ≥« –ĶńĻķľ ĪÍ◊ľ Īľš£®Ķ•őĽ£ļ–° Ī£©Ņ…‘ŕ ż÷Š…ŌĪŪ ĺ»ÁŌ¬£ļ ![]()
»ÁĻŻĹęŃĹĶōĻķľ ĪÍ◊ľ ĪľšĶń≤ÓľÚ≥∆ő™ Ī≤Ó£¨ń«√īŌ¬Ń–ňĶ∑®÷–’ż»∑Ķń «£® £©
A. ļļ≥«”ŽŇ¶‘ľĶń Ī≤Óő™13–° Ī B. ĪĪĺ©”ŽŇ¶‘ľĶń Ī≤Óő™13–° Ī
C. ĪĪĺ©”ŽŇ¶‘ľĶń Ī≤Óő™14–° Ī D. ĪĪĺ©”Ž∂ŗ¬◊∂ŗĶń Ī≤Óő™14–° Ī
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
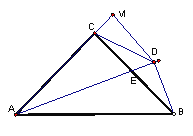
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕ°ųABC÷–£¨AC=BC£¨°ŌACB=900£¨AE∆Ĺ∑÷°ŌBACĹĽBC”ŕE£¨BD°ÕAE”ŕD£¨DM°ÕACĹĽACĶń—”≥§ŌŖ”ŕM£¨Ń¨Ĺ”CD°£Ō¬Ń–ĹŠ¬Ř£ļ
ĘŔAC+CE=AB£ĽĘŕCD= ![]() £¨ĘŘ°ŌCDA=450 £¨Ę‹
£¨ĘŘ°ŌCDA=450 £¨Ę‹![]() ő™∂®÷Ķ°£
ő™∂®÷Ķ°£
∆š÷–’ż»∑ĶńĹŠ¬Ř”–£®°°°°£©
A.1łŲ B.2łŲ C.3łŲ D.4łŲ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨Ĺę“Ľ’ŇĶ»ĪŖ»żĹ«–ő÷Ĺ∆¨—ō÷–őĽŌŖľŰ≥…4łŲ–°»żĹ«–ő£¨≥∆ő™Ķŕ“Ľīő≤Ŕ◊ų£Ľ»Ľļů£¨Ĺę∆š÷–Ķń“ĽłŲ»żĹ«–őįīÕ¨—ý∑Ĺ Ĺ‘ŔľŰ≥…4łŲ–°»żĹ«–ő£¨Ļ≤Ķ√ĶĹ7łŲ–°»żĹ«–ő£¨≥∆ő™Ķŕ∂Ģīő≤Ŕ◊ų£Ľ‘ŔĹę∆š÷–“ĽłŲ»żĹ«–őįīÕ¨—ý∑Ĺ Ĺ‘ŔľŰ≥…4łŲ–°»żĹ«–ő£¨Ļ≤Ķ√ĶĹ10łŲ–°»żĹ«–ő£¨≥∆ő™Ķ໿īő≤Ŕ◊ų£Ľ°≠łý囓‘…Ō≤Ŕ◊ų£¨»Ű“™Ķ√ĶĹ1000łŲ–°»żĹ«–ő£¨‘Ú–Ť“™≤Ŕ◊ųĶńīő ż «( )
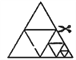
A. 332 B. 333 C. 334 D. 335
≤ťŅīīūįłļÕĹ‚őŲ>>
įŔ∂»÷¬–Ň - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com