
【题目】已知,如图在△ABC中,AD、BE分别是BC,AC边上的高,AD、BE交于H,DA=DB,BH=AC,点F为BH的中点,∠ABE=15°.
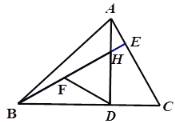
(1)求证:△ADC≌△BDH
(2)求证:DC=DF
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:
【题目】等腰直角三角形ABC,AB=AC,∠BAC=∠BDC=90°,

(1)若∠DBA=20°,则∠ACD=______°;
(2)连接AD,则∠ADB=______°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是我们生活中经常接触的小刀,刀片的外壳是四边形,而且刀片外壳与刀片铆合部分都是直角,刀片的上、下是平行的,转动刀片时会形成∠1和∠2,则∠1+∠2的度数为( )

A. 80° B. 70° C. 90° D. 100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,AD是△ABC的中线.△ABD与△ACD的面积有怎样的数量关系?为什么?

(2)若三角形的面积记为S,例如:△ABC的面积记为S△ABC.如图②,已知S△ABC=1.△ABC的中线AD、CE相交于点O,求四边形BDOE的面积.

小华利用(1)的结论,解决了上述问题,解法如下:
连接BO,设S△BEO=x,S△BDO=y,由(1)结论可得:S△BCE=S△BAD=![]() S△ABC=
S△ABC=![]() ,S△BCO=2S△BDO=2y,S△BAO=2S△BEO=2x.则有
,S△BCO=2S△BDO=2y,S△BAO=2S△BEO=2x.则有 即
即 所以x+y=
所以x+y=![]() .即四边形BDOE面积为
.即四边形BDOE面积为![]() .
.
请仿照上面的方法,解决下列问题:
①如图③,已知S△ABC=1.D、E是BC边上的三等分点,F、G是AB边上的三等分点,AD、CF交于点O,求四边形BDOF的面积.

②如图④,已知S△ABC=1.D、E、F是BC边上的四等分点,G、H、I是AB边上的四等分点,AD、CG交于点O,则四边形BDOG的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,∠BED=61°,∠ABE的平分线与∠CDE的平分线交于点F,则∠DFB=( )

A. 149° B. 149.5° C. 150° D. 150.5°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线l:y=2kx-4k+3(k≠0)恒过某一定点P.
(1)求该定点P的坐标;
(2)已知点A、B坐标分别为(0,1)、(2,1),若直线l与线段AB相交,求k的取值范围;
(3)在0≤x≤2范围内,任取3个自变量x1,x2、x3,它们对应的函数值分别为y1、y2、y3,若以y1、y2、y3为长度的3条线段能围成三角形,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面结论:
①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,
其中结论正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连接AD,AE,△ADE的周长为12cm.
(1)求BC的长;
(2)分别连接OA,OB,OC,若△OBC的周长为26cm,求OA的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com