
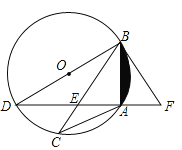
【题目】如图,△ABC内接于⊙O,且AB=AC,BD是⊙O的直径,AD与BC交于点E,F在DA的延长线上,且BF=BE.
(1)试判断BF与⊙O的位置关系,并说明理由;
(2)若BF=6,∠C=30°,求阴影的面积.
【答案】(1)相切; ![]()
【解析】
(1)根据等腰三角形性质求出∠FBA=∠EBA=∠C,推出∠D=∠C=∠FBA,根据∠DAB=90°推出∠D+∠DBA=90°,求出∠ABD+∠FBA=90°,根据切线的判定推出即可.
(2)连接OA,求出∠BOA=60°,求出AB长,求出BD、AD,求出OB,根据三角形的面积求出△ABD面积,即可求出△BAO面积,求出扇形BOA面积,即可求出答案.
(1)解:BF与⊙O的位置关系是相切,
理由是:∵∠D和∠C都对弧AB,
∴∠C=∠D,
∵BD是直径,
∴∠DAB=90°,
∴∠D+∠ABD=90°,
∴∠C+∠ABD=90°,
∵∠DAB=90°,
∴BA⊥EF,
∵BE=BF,
∴∠EBA=∠FBA,
∵AB=AC,
∴∠C=∠EBA=∠FBA,
∵∠C+∠ABD=90°(已证),
∴∠FBA+∠ABD=90°,
∴∠FBD=90°,
∵OB是半径,
∴BF是⊙O的切线,
即BF与⊙O的位置关系是相切;
(2)解:连接OA,

∵∠C=∠D=30°=∠FBA,
∴在Rt△ABF中,BF=6,AF=![]() BF=3,
BF=3,
由勾股定理得AB=3![]() ,
,
在Rt△DBA中,∠D=30°,
∴BD=2AB=6![]() ,OB=3
,OB=3![]()
,∠BOA=2∠C=60°,
∵在Rt△ABD中,BD=6![]() ,OB=3
,OB=3![]() ,
,
由勾股定理得:AD=9,
又∵BO=OD,
∴根据等底同高的三角形的面积相等得出S△BOA=S△AOD=![]()
![]() ,
,
∠BOA=2∠C=60°,
∴S阴影=S扇形OBA-S△OAB=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】中华文明,源远流长,中华汉字,寓意深广,为了传承优秀传统文化,某校九年级组织600名学生参加了一次“汉字听写”大赛![]() 赛后发现所有参赛学生的成绩均不低于60分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩作为样本,成绩如下:
赛后发现所有参赛学生的成绩均不低于60分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩作为样本,成绩如下:
90,92,81,82,78,95,86,88,72,66,62,68,89,86,93,97,100,73,76,80,77,81,86,89,82,85,71,68,74,98,90,97,100,84,87,73,65,92,96,60.
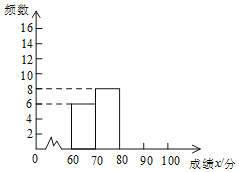
对上述成绩进行了整理,得到下列不完整的统计图表:
成绩 | 频数 | 频率 |
| 6 |
|
| 8 |
|
| a | b |
| c | d |
请根据所给信息,解答下列问题:
![]() ______,
______,![]() ______,
______,![]() ______,
______,![]() ______;
______;
![]() 请补全频数分布直方图;
请补全频数分布直方图;
![]() 若成绩在90分以上
若成绩在90分以上![]() 包括90分
包括90分![]() 的为“优”等,请你估计参加这次比赛的600名学生中成绩“优”等的约有多少人?
的为“优”等,请你估计参加这次比赛的600名学生中成绩“优”等的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前“微信”、“支付宝”、“共享单车”和“网购”给我们的生活带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行调查,随机调查了m人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.

(1)根据图中信息求出m=______,n=______;
(2)请你帮助他们将这两个统计图补全;
(3)根据抽样调查的结果,请估算全校2000名学生中,大约有多少人最认可“微信”这一新生事物?
查看答案和解析>>
科目:初中数学 来源: 题型:
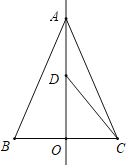
【题目】如图,等腰△ABC中,AB=AC=3,BC=2,BC边上的高AO,点D为射线AO上一点,一动点P从点A出发,沿AD﹣DC运动,到达点C停止,动点P在AD上运动速度为3个单位每秒,动点P在CD上运动速度为1个单位每秒,则当AD=____时,运动时间最短.
查看答案和解析>>
科目:初中数学 来源: 题型:
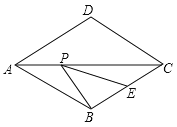
【题目】如图,菱形ABCD的边长为4,∠DAB=60°,E为BC的中点,在对角线AC上存在一点P,使△PBE的周长最小,则△PBE的周长的最小值为( )
A. ![]() +1B.
+1B. ![]() C.
C. ![]() +1D.
+1D. ![]() +2
+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园手机”现象越来越受到社会的关注。春节期间,小明随机调查了城区若干名同学和家长对中学生带手机现象的看法.统计整理并制作了如下的统计图:
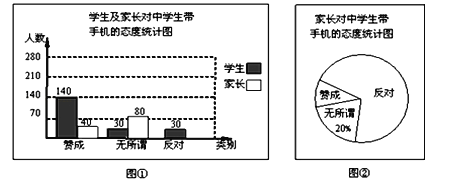
(1)这次的调查对象中,学生和家长共有 人;
(2)图②中表示家长“赞成”的圆心角的度数为 度;
(3)已知某地区共6500名家长,估计其中反对中学生带手机的大约有多少名家长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,对于P(a,b),若点P'的坐标为(ka+b, ![]() )(其中k为常数且k≠0),则称点P'为点P的“k的和谐点” .已知点A在函数
)(其中k为常数且k≠0),则称点P'为点P的“k的和谐点” .已知点A在函数![]() 的图像上运动,且点A是点B的“
的图像上运动,且点A是点B的“![]() 的和谐点”,若Q(-2, 0),则BQ的最小值为_______.
的和谐点”,若Q(-2, 0),则BQ的最小值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂计划生产A、B两种产品共60件,需购买甲、乙两种材料,生产一件A产品需甲种材料4千克,乙种材料1千克;生产一件B产品需甲、乙两种材料各3千克,经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.
(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂生产的B产品不少于38件且不多于40件,若希望用于购买甲、乙两种材料的资金最少,应如何安排生产?最少购买资金是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中∠C=90°,∠BAC=30°,AB=8,以2![]() 为边长的正方形DEFG的一边GD在直线AB上,且点D与点A重合,现将正方形DEFG沿A﹣B的方向以每秒1个单位的速度匀速运动,当点D与点B重合时停止,则在这个运动过程中,正方形DEFG与△ABC的重合部分的面积S与运动时间t之间的函数关系图象大致是( )
为边长的正方形DEFG的一边GD在直线AB上,且点D与点A重合,现将正方形DEFG沿A﹣B的方向以每秒1个单位的速度匀速运动,当点D与点B重合时停止,则在这个运动过程中,正方形DEFG与△ABC的重合部分的面积S与运动时间t之间的函数关系图象大致是( )

A. 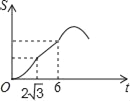 B.
B. 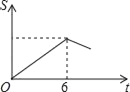 C.
C. 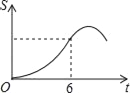 D.
D. 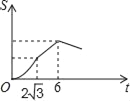
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com