
| 消费卡 | 消费方式 |
| 普通卡 | 35元/次 |
| 白金卡 | 280元/张,凭卡免费消费10次再送2次 |
| 钻石卡 | 560元/张,凭卡每次消费不再收费 |
分析 (Ⅰ)根据普通消费方式,算出健身6次的费用,再与280、560进行比较,即可得出结论;
(Ⅱ)根据“普通消费费用=35×次数”即可得出y普通关于x的函数关系式;再根据“白金卡消费费用=卡费+超出部分的费用”即可得出y白金卡关于x的函数关系式;
(Ⅲ)先算出健身18次普通消费和白金卡消费两种形式下的费用,再令白金卡消费费用=钻石卡消费的卡费,算出二者相等时的健身次数,由此即可得出结论.
解答 解:(Ⅰ)35×6=210(元),
∵210<280<560,
∴选择普通消费方式更合算.
(Ⅱ)根据题意得:y普通=35x.
当x≤12时,y白金卡=280;当x>12时,y白金卡=280+35(x-12)=35x-140.
∴y白金卡=$\left\{\begin{array}{l}{280(x≤12)}\\{35x-140(x>12)}\end{array}\right.$.
(Ⅲ)当x=18时,y普通=35×18=630;y白金卡=35×18-140=490;
令y白金卡=560,即35x-140=560,
解得:x=20.
当18≤x≤19时,选择白金卡消费最合算;当x=20时,选择白金卡消费和钻石卡消费费用相同;当x≥21时,选择钻石卡消费最合算.
点评 本题考查了一次函数的应用,解题的关键是:(Ⅰ)根据数量关系列式计算;(Ⅱ)根据数量关系找出函数关系式;(Ⅲ)令y白金卡=560,算出白金卡消费和钻石卡消费费用相同时健身的次数.本题属于基础题,难度不大,解决该题型题目时,根据数量关系列式计算(或列出函数关系式)是关键.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:选择题
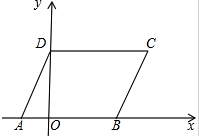 如图所示,平行四边形ABCD中,顶点A,B,D在坐标轴上,AD=5,AB=9,点A的坐标为(-3,0),则点C的坐标为( )
如图所示,平行四边形ABCD中,顶点A,B,D在坐标轴上,AD=5,AB=9,点A的坐标为(-3,0),则点C的坐标为( )| A. | (6,5) | B. | (9,4) | C. | (6,4) | D. | (9,5) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知矩形ABCD中,AB=6cm,BC=8cm,E,F,G,H分别是AB,BC,CD,DA的中点,则四边形EFGH的周长等于20cm.
如图,已知矩形ABCD中,AB=6cm,BC=8cm,E,F,G,H分别是AB,BC,CD,DA的中点,则四边形EFGH的周长等于20cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com