
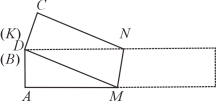
【题目】 如图,ABCD是一张矩形纸片,AD=BC=1,AB=CD=5.在矩形ABCD的边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,使MB与DN交于点K,得到△MNK.

(1)若∠1=70°,求∠MKN的度数.
(2)△MNK的面积能否小于![]() ?若能,求出此时∠1的度数;若不能,试说明理由.
?若能,求出此时∠1的度数;若不能,试说明理由.
(3)如何折叠能够使△MNK的面积最大?请你利用备用图探究可能出现的情况,求出最大值.

【答案】40°;不能;1.3
【解析】
试题分析:根据折叠图形的性质求出角的度数;过M点作ME⊥DN,垂足为点E,则ME=AD=1,然后得出三角形的面积大于等于![]() 即可得出答案;分两种情况进行讨论计算,得出最大值.
即可得出答案;分两种情况进行讨论计算,得出最大值.
试题解析:(1)40°
(2)不能. 过M点作ME⊥DN,垂足为点E,则ME=AD=1, 由(1)知∠KNM=∠KMN.∴MK=NK.
又MK≥ME, ∴NK≥1. ∴![]() .
.
∴△MNK的面积最小值为![]() ,不可能小于
,不可能小于![]() .
.
(3)分两种情况:
情况一:将矩形纸片对折,使点B与点D重合,此时点K也与点D重合.
设MK=MD=x,则AM=5-x,由勾股定理,得
![]() ,
,
解得,![]() .即
.即![]() .
.
∴![]() .
.
 情况二:将矩形纸片沿对角线AC对折,此时折痕为AC.
情况二:将矩形纸片沿对角线AC对折,此时折痕为AC.
设MK=AK= CK=x,则DK=5-x,同理可得
即![]() .
.
∴![]() .
.
∴△MNK的面积最大值为1.3.


科目:初中数学 来源: 题型:
【题目】计算:(1)(-2)3+(π+3)0-(![]() )-3 (2)(-2a2b3)4+(-a)8·(2b4)3
)-3 (2)(-2a2b3)4+(-a)8·(2b4)3
(3)![]() (4) (2x+y)(2x-y)-(2x-y)2.
(4) (2x+y)(2x-y)-(2x-y)2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,D为边BC上一点,将线段AB平移至DE,连接AE、AD、EC.
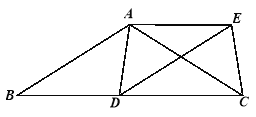
(1)求证:AD=EC;
(2)当点D在什么位置时,四边形ADCE是矩形,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,最适合采用全面调查(普查)方式的是( )
A. 对中央电视台2019年春节联欢晚会满意度的调查
B. 对某品牌手机电池待机时间的调查
C. 对全国中学生观看电影《流浪地球》情况的调查
D. 对“神州十一号”飞船零部件安全性的调查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于特殊四边形对角线的性质,矩形具备而平行四边形不一定具备的是( )
A. 对角线互相平分B. 对角线互相垂直
C. 对角线相等D. 对角线平分一组对角
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是矩形ABCD的边BC上一点,EF⊥AE,EF分别交AC、CD于点M、F,BG⊥AC,垂足为G,BG交AE于点H。
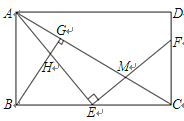
(1)求证:△ABE∽△ECF;
(2)找出与△ABH相似的三角形,并证明;
(3)若E是BC中点,BC=2AB,AB=2,求EM的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com