
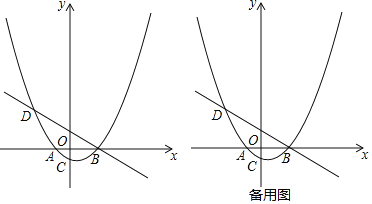
����Ŀ����ͼ����֪������y=a��x+2����x-4����aΪ��������a��0����x������������ν���A��B���㣬��y�ύ�ڵ�C��������B��ֱ��y=-![]() x+b�������ߵ���һ����ΪD���ҵ�D�ĺ�����Ϊ-5��
x+b�������ߵ���һ����ΪD���ҵ�D�ĺ�����Ϊ-5��
��1���������ߵĺ�������ʽ��
��2��PΪֱ��BD�·����������ϵ�һ�㣬����PD��PB�����PBD��������ֵ��
��3����FΪ�߶�BD��һ�㣨�����˵㣩������AF��һ����M�ӵ�A���������߶�AF��ÿ��1����λ���ٶ��˶���F�������߶�FD��ÿ��2����λ���ٶ��˶���D��ֹͣ������F�������Ƕ���ʱ����M�������˶���������ʱ���٣�
���𰸡���1��![]() ����2��
����2��![]() ����3����-2��2
����3����-2��2![]() ��
��
��������
��1�����������A��B���꣬Ȼ�����ֱ��BD�Ľ���ʽ����õ�D���꣬���������߽���ʽ�����a��ֵ��
��2���������ε������ʽ����������ϵʽ����ȷ�������ֵ��
��3�������⣬����M�˶���·��Ϊ����AF+DF���˶�ʱ�䣺t=AF+![]() DF����ͼ���������ߣ���AF+
DF����ͼ���������ߣ���AF+![]() DFת��ΪAF+FG�����ɴ��߶���̣��õ����߶�AH��ֱ��BD�Ľ��㣬��Ϊ�����F�㣮
DFת��ΪAF+FG�����ɴ��߶���̣��õ����߶�AH��ֱ��BD�Ľ��㣬��Ϊ�����F�㣮
��1��������y=a��x+2����x-4������y=0�����x=-2��x=4��
��A��-2��0����B��4��0����
��ֱ��y=-![]() x+b������B��4��0����
x+b������B��4��0����
��-![]() ��4+b=0�����b=
��4+b=0�����b=![]() ��
��
��ֱ��BD����ʽΪ��y=-![]() x+
x+![]() ��
��
��x=-5ʱ��y=3![]() ��
��
��D��-5��3![]() ����
����
�ߵ�D��-5��3![]() ����������y=a��x+2����x-4���ϣ�
����������y=a��x+2����x-4���ϣ�
��a��-5+2����-5-4��=3![]() ��
��
��a=![]() ��
��
�������ߵĺ�������ʽΪ��y=![]() x2-
x2-![]() x-
x-![]()
��2����P��m��![]() m2-
m2-![]() m-
m-![]() ��
��
��S��BPD=![]() ��9[��-
��9[��-![]() m+
m+![]() ��-��
��-��![]() m2-
m2-![]() m-
m-![]() ��]
��]
=-![]() m2-
m2-![]() m+10
m+10![]()
=-![]() ��m+
��m+![]() ��2+
��2+![]()
���BPD��������ֵΪ![]() ��
��
��3����ͼ��

��DK��AB��AH��DK��AH��ֱ��BD�ڵ�F��
���ɣ�2���ã�DN=3![]() ��BN=9��
��BN=9��
�ߡ�DBA=30�㣬
���BDH=30�㣬
��FG=DF��sin30��=![]() FD��
FD��
�൱�ҽ���AH��DKʱ��AF+FH��С��
��M�������˶�����ʱΪ��t=AF+![]() FD=AF+FH��
FD=AF+FH��
��lBD��y=-![]() x+
x+![]() ��
��
��Fx=Ax=-2��F��-2��2![]() ��
��
�൱F����Ϊ��-2��2![]() ��ʱ����ʱ���٣�
��ʱ����ʱ���٣�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
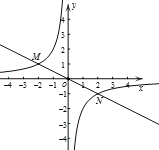
����Ŀ����ͼ������������![]() ��ͼ����һ�κ���
��ͼ����һ�κ���![]() ��ͼ��ֱ���M��N���㣬��֪��M(-2��m).
��ͼ��ֱ���M��N���㣬��֪��M(-2��m).
(1)���������ı���ʽ��
(2)��PΪy���ϵ�һ�㣬����MPNΪֱ��ʱ��ֱ��д����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
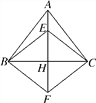
����Ŀ����ͼ���ڵ���������ABC�У�AB=AC��AH��BC����E��AH��һ�㣬�ӳ�AH����F��ʹFH=EH.
(1)��֤���ı���EBFC�����Σ�
(2)�����BAC=��ECF����֤��AC��CF.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
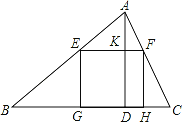
����Ŀ����ͼ��һ����ϵ���״�����������ABC����BC=120mm����AD=80mm�������ӹ��ɾ��������ʹ���ε�һ����BC�ϣ�������������ֱ���AB��AC�ϣ���EG=x mm��EF=y mm��
��1��д��x��y�Ĺ�ϵʽ��
��2����S��ʾ����EGHF�������ijͬѧ˵������EGHFΪ������ʱS������˵����ȷ��˵�����ɣ������S�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
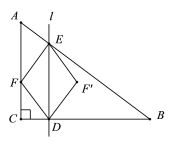
����Ŀ����ͼ����Rt��ABC��, ![]() ��
��![]() ��
��![]() ��ֱ��l����AC�غϵ�λ�ÿ�ʼ��ÿ��
��ֱ��l����AC�غϵ�λ�ÿ�ʼ��ÿ��![]() ����λ���ٶ���CB����ƽ���ƶ����ҷֱ���CB��AB�߽���D��E���㣬����F��A��ʼ������AC
����λ���ٶ���CB����ƽ���ƶ����ҷֱ���CB��AB�߽���D��E���㣬����F��A��ʼ������AC![]() CB
CB![]() BA�˶�����F��AC��CB��BA�����˶����ٶȷֱ�Ϊÿ��3��4��5����λ����F��ֱ��lͬʱ���������˶���ʱ��Ϊt�룬����F��һ�λص���Aʱ����F��ֱ�� lͬʱֹͣ�˶����˶������У�����F����ֱ��DE�ĶԳƵ㣬��Ϊ��
BA�˶�����F��AC��CB��BA�����˶����ٶȷֱ�Ϊÿ��3��4��5����λ����F��ֱ��lͬʱ���������˶���ʱ��Ϊt�룬����F��һ�λص���Aʱ����F��ֱ�� lͬʱֹͣ�˶����˶������У�����F����ֱ��DE�ĶԳƵ㣬��Ϊ��![]() �����γɵ��ı���
�����γɵ��ı���![]() Ϊ���Σ�����������������
Ϊ���Σ�����������������![]() ֮��Ϊ_________��
֮��Ϊ_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��l1��y����![]() x�뷴��������y��
x�뷴��������y��![]() ��ͼ����A��B���㣨��A�ڵ�B��ࣩ����֪A�����������2��
��ͼ����A��B���㣨��A�ڵ�B��ࣩ����֪A�����������2��
��1�����������ı���ʽ��
��2������ͼ��ֱ��д����![]() x��
x��![]() �Ľ⼯��
�Ľ⼯��
��3����ֱ��l1��y��- ![]() x��y����ƽ�ƺ��ֱ��l2�뷴��������y��
x��y����ƽ�ƺ��ֱ��l2�뷴��������y��![]() �ڵڶ������ڽ��ڵ�C�������ABC�����Ϊ30����ƽ�ƺ��ֱ��l2�ĺ�������ʽ��
�ڵڶ������ڽ��ڵ�C�������ABC�����Ϊ30����ƽ�ƺ��ֱ��l2�ĺ�������ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
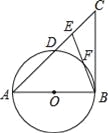
����Ŀ����ͼ������ABC�У�E��AC���ϵ�һ�㣬��AE=AB����BAC=2��CBE����ABΪֱ������O��AC�ڵ�D����BE�ڵ�F��
��1����֤��BC����O�����ߣ�
��2����AB=8��BC=6����DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾������ij�ֲ�Ʒÿ���ɱ�Ϊ40Ԫ�����г�����������������Ϣ��
�ٸò�Ʒ90��������������m������ʱ�䣨��x�죩����һ�κ�����ϵ�������������±���
ʱ�䣨��x�죩 | 1 | 3 | 6 | 10 | �� |
����������m���� | 198 | 194 | 188 | 180 | �� |
�ڸò�Ʒ90����ÿ������ۼ۸���ʱ�䣨��x�죩�Ĺ�ϵ���±���
ʱ�䣨��x�죩 | 1��x��50 | 50��x��90 |
���ۼ۸�Ԫ/���� | x+60 | 100 |
��1����m����x��һ�κ�������ʽ��
��2�������۸ò�Ʒÿ������ΪyԪ����д��y����x�ĺ�������ʽ���������90���ڸò�Ʒ������������������������Ƕ��٣�����ʾ��ÿ����������=������������ÿ�����ۼ۸�-ÿ���ɱ�����
��3���ڸò�Ʒ���۵Ĺ����У����ж���������������5400Ԫ����ֱ��д�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ѧ���
���ȱ������ε���������D��E��F�ֱ�����ABC���������������dzƵȱ�������DEF����ABC���ڽ�����������
�����������
��1������ͼ����DEF��Ϊ�ȱ�����������������DEF����ABC���ڽ��������ε��� ��
A��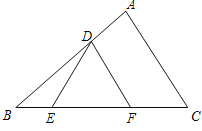 ��������B��
��������B��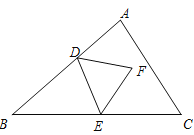
C��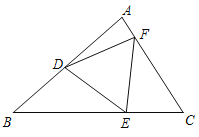
��������֤��
��2����ͼ��������ABC������B��60�㣬DΪ��AB��һ������BC��BD����DE��DB��EMƽ����DEC������AC�ڵ�M����DME�����Բ���BC����һ������ΪN��
��֤����DMN����ABC���ڽ�����������
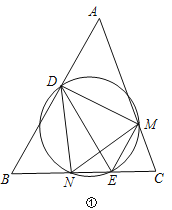
��֪ʶӦ�ã�
��3����ͼ��������ABC������B��60�㣬��A��45�㣬BC��2��D�DZ�AB�ϵĶ���������BC�ϴ���һ��E��ʹ����DEΪ�ߵĵȱ�������DEF����ABC���ڽ��������Σ�����DEF�����Բ��O���BC����һ������ΪK����DK�����ֵΪ ����СֵΪ ��
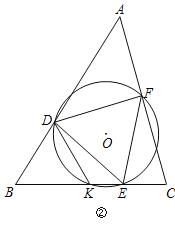
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com