
【题目】如图,已知直线AB和CD相交于点O,∠COE=90°,OF平分∠AOE,∠COF=24°,求∠BOD的度数. 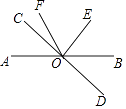
【答案】解:∵∠COF=24°,∠COE=90°, ∴∠EOF=∠COE﹣∠COF=90°﹣24°=66°,
∵OF平分∠AOE,
∴∠AOE=2∠EOF=66°×2=132°,
∴∠BOE=180°﹣132°=48°,
∵∠BOD=∠DOE﹣∠BOE=90°﹣48°=42°
【解析】直接利用角平分线的性质得出∠AOE的度数,进而得出∠BOE的度数,即可得出答案.
【考点精析】本题主要考查了角的平分线和对顶角和邻补角的相关知识点,需要掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个才能正确解答此题.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】安宁市的一种绿色蔬菜,若在市场上直接销售,每吨利润为1000元,若经粗加工后销售,每吨利润可达4500元;若经精加工后销售每吨获利7500元.当地一家农产品企业收购这种蔬菜140吨,该企业加工厂的生产能力是:如果对蔬菜进行粗加工,每天可以加工16吨,如果进行精加工,每天可加工6吨,但两种加工方式不能同时进行,受季节条件限制,企业必须在15天的时间将这批蔬菜全部销售或加工完毕,企业研制了四种可行方案: 方案一:全部直接销售;
方案二:全部进行粗加工;
方案三:尽可能多地进行精加工,没有来得及进行精加工的直接销售;
方案四:将一部分进行精加工,其余的进行粗加工,并恰好15天完成.
请通过计算以上四个方案的利润,帮助企业选择一个最佳方案使所获利润最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展阳光体育活动,要求每名学生从以下球类活动中选择一项参加体育锻炼:A﹣乒乓球;B﹣足球;C﹣篮球;D﹣羽毛球.学校王老师对八年级某班同学的活动选择情况进行调查统计,绘制了两幅不完整的统计图,如图所示.
(1)请你求出该班学生的人数并补全条形统计图;
(2)已知该校八年级学生共有500人,学校根据统计调查结果进行预估,按参加项目人数每10人购买一个训练用球的标准,为B,C两个项目统一购买训练用球.经了解,某商场销售的足球比篮球的单价少30元,此时学校共需花费2700元购买足球和篮球.求该商场销售的足球和篮球的单价.
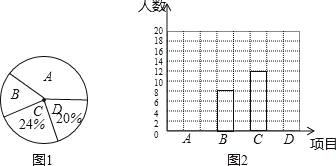
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD,BE分别为边BC,AC上的高线,D,E为垂足,M为AB的中点,N为DE的中点.求证:
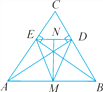
(1)△MDE是等腰三角形.
(2)MN⊥DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校一块空地被荒废,如图,为了绿化环境,学校打算利用这块空地种植花草,已知AB⊥BC,CD⊥BC,AB=![]() CD=
CD=![]() m,BC=3
m,BC=3![]() m,试求这块空地的面积.
m,试求这块空地的面积.
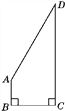
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com