
 小明家门前有一块空地,空地外有一面长10米的围墙,为了美化生活环境,小明的爸爸准备靠墙修建一个矩形花圃,他买回了32米长的不锈钢管准备作为花圃的围栏(如图所示),花圃的一边AD(垂直围墙的边)究竟应为多少米才能使花圃的面积最大?
小明家门前有一块空地,空地外有一面长10米的围墙,为了美化生活环境,小明的爸爸准备靠墙修建一个矩形花圃,他买回了32米长的不锈钢管准备作为花圃的围栏(如图所示),花圃的一边AD(垂直围墙的边)究竟应为多少米才能使花圃的面积最大? 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
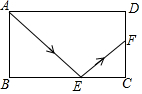 如图,已知矩形ABCD中,AB=2,BC=3,F是CD的中点,一束光线从点A出发,通过BC边反射,恰好经过点F,那么反射点E与点C的距离为( )
如图,已知矩形ABCD中,AB=2,BC=3,F是CD的中点,一束光线从点A出发,通过BC边反射,恰好经过点F,那么反射点E与点C的距离为( )| A. | 1 | B. | 2 | C. | 1或2 | D. | 1.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | -4 | C. | 2 | D. | -2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com