
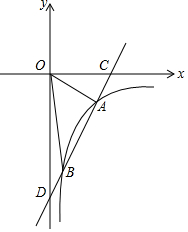
 ��ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=ax+b��a��0���뷴��������y=$\frac{k}{x}$��k��0��x��0������A��B���㣬��x�ᡢy��ֱ���C��D���㣬����OA��OB����OA=2$\sqrt{13}$��sin��AOC=$\frac{2\sqrt{13}}{13}$����B������Ϊ��m��-8��
��ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=ax+b��a��0���뷴��������y=$\frac{k}{x}$��k��0��x��0������A��B���㣬��x�ᡢy��ֱ���C��D���㣬����OA��OB����OA=2$\sqrt{13}$��sin��AOC=$\frac{2\sqrt{13}}{13}$����B������Ϊ��m��-8������ ��1���������������A�����꣬���뷴������������ʽ�����k������÷�������������ʽ��������B�����꣬�ٰ�A��B�����������һ�κ�������ʽ����ô𰸣�
��2����P������Ϊ��0��y������B����������OB�ij�����ɵõ�OP=OB��OB=BP���ɵõ�����y�ķ��̣������y��ֵ�������P�����꣮
��� �⣺
��1����A��AE��y���ڵ�E����ͼ��
��OA=2$\sqrt{13}$��sin��AOC=$\frac{2\sqrt{13}}{13}$��
��$\frac{AE}{OA}$=$\frac{2\sqrt{13}}{13}$����$\frac{AE}{2\sqrt{13}}$=$\frac{2\sqrt{13}}{13}$�����AE=4��
��AE=$\sqrt{O{A}^{2}-A{E}^{2}}$=6��
��A��6��-4����
�߷���������y=$\frac{k}{x}$��k��0��x��0����A�㣬
��k=-4��6=-24��
�෴������������ʽΪy=-$\frac{24}{x}$��
�߷���������y=$\frac{k}{x}$��k��0��x��0������B�㣬
��-8m=-24�����m=3��
��B��3��-8����
��һ�κ���y=ax+b��a��0����A��B���㣬
��$\left\{\begin{array}{l}{6a+b=-4}\\{3a+b=-8}\end{array}\right.$�����$\left\{\begin{array}{l}{a=\frac{4}{3}}\\{b=-12}\end{array}\right.$��
��һ�κ�������ʽΪy=$\frac{4}{3}$x-12��
��2����B��3��-8����
��OB=$\sqrt{{3}^{2}+��-8��^{2}}$=$\sqrt{73}$��
��P��������0��y������OP=|y|��PB=$\sqrt{{3}^{2}+��y+8��^{2}}$��
�ߡ�BOP����OBΪ���ĵ��������Σ�
��OP=OB��PB=OB��
��OP=OBʱ������|y|=$\sqrt{73}$�����y=��$\sqrt{73}$��
��ʱP������Ϊ��0��$\sqrt{73}$����0��-$\sqrt{73}$����
��PB=OBʱ������$\sqrt{{3}^{2}+��y+8��^{2}}$=$\sqrt{73}$�����y=-16��y=0����ȥ����
��ʱP������Ϊ��0��-16����
���Ͽ�֪���������ĵ�P������Ϊ��0��$\sqrt{73}$����0��-$\sqrt{73}$����0��-16����
���� ������Ҫ���鷴����������һ�κ����Ľ������⣬���պ���ͼ��Ľ�����������ÿһ����������ʽ�ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
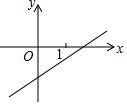 һ�κ���y=kx+b��ͼ����ͼ��ʾ���������ж���ȷ���ǣ�������
һ�κ���y=kx+b��ͼ����ͼ��ʾ���������ж���ȷ���ǣ�������| A�� | |k|��|b| | B�� | |k|��|b| | ||
| C�� | |k|=|b| | D�� | |k|��|b|�Ĵ�С��ϵ����ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ƽ��ֱ�������У�OA=4��OB=8��ֱ��y=-2x+b��x���y���ڵ�D��E��
��ƽ��ֱ�������У�OA=4��OB=8��ֱ��y=-2x+b��x���y���ڵ�D��E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
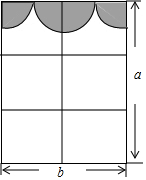 ij���䴰����ͼ��ʾ�������Ϸ���װ�����������ķ�֮һԲ��һ����Բ��ɣ����ǵİ뾶��ͬ����
ij���䴰����ͼ��ʾ�������Ϸ���װ�����������ķ�֮һԲ��һ����Բ��ɣ����ǵİ뾶��ͬ�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com