
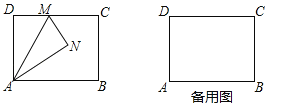
【题目】如图,矩形ABCD中,AB=4,AD=3,M是边CD上一点,将△ADM沿直线AM对折,得到△ANM.
(1)当AN平分∠MAB时,求DM的长;
(2)连接BN,当DM=1时,求△ABN的面积;
(3)当射线BN交线段CD于点F时,求DF的最大值.
【答案】(1)DM=![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)由折叠性质得∠MAN=∠DAM,证出∠DAM=∠MAN=∠NAB,由三角函数得出DM=ADtan∠DAM=![]() 即可;
即可;
(2)延长MN交AB延长线于点Q,由矩形的性质得出∠DMA=∠MAQ,由折叠性质得出∠DMA=∠AMQ,AN=AD=3,MN=MD=1,得出∠MAQ=∠AMQ,证出MQ=AQ,设NQ=x,则AQ=MQ=1+x,证出∠ANQ=90°,在Rt△ANQ中,由勾股定理得出方程,解方程求出NQ=4,AQ=5,即可求出△ABN的面积;
(3)过点A作AH⊥BF于点H,证明△ABH∽△BFC,得出对应边成比例![]() ,得出当点N、H重合(即AH=AN)时,AH最大,BH最小,CF最小,DF最大,此时点M、F重合,B、N、M三点共线,由折叠性质得:AD=AH,由AAS证明△ABH≌△BFC,得出CF=BH,由勾股定理求出BH,得出CF,即可得出结果.
,得出当点N、H重合(即AH=AN)时,AH最大,BH最小,CF最小,DF最大,此时点M、F重合,B、N、M三点共线,由折叠性质得:AD=AH,由AAS证明△ABH≌△BFC,得出CF=BH,由勾股定理求出BH,得出CF,即可得出结果.
试题解析:(1)由折叠性质得:△ANM≌△ADM,∴∠MAN=∠DAM,∵AN平分∠MAB,∠MAN=∠NAB,∴∠DAM=∠MAN=∠NAB,∵四边形ABCD是矩形,∴∠DAB=90°,∴∠DAM=30°,∴DM=ADtan∠DAM=3×tan30°=![]() =
=![]() ;
;
(2)延长MN交AB延长线于点Q,如图1所示,∵四边形ABCD是矩形,∴AB∥DC,∴∠DMA=∠MAQ,由折叠性质得:△ANM≌△ADM,∴∠DMA=∠AMQ,AN=AD=3,MN=MD=1,∴∠MAQ=∠AMQ,∴MQ=AQ,设NQ=x,则AQ=MQ=1+x,∵∠ANM=90°,∴∠ANQ=90°,在Rt△ANQ中,由勾股定理得:![]() ,∴
,∴![]() ,解得:x=4,∴NQ=4,AQ=5,∵AB=4,AQ=5,∴S△NAB=
,解得:x=4,∴NQ=4,AQ=5,∵AB=4,AQ=5,∴S△NAB=![]() =
=![]() =
=![]() ANNQ=
ANNQ=![]() ;
;
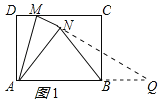
(3)过点A作AH⊥BF于点H,如图2所示,∵四边形ABCD是矩形,∴AB∥DC,∴∠HBA=∠BFC,∵∠AHB=∠BCF=90°,∴△ABH∽△BFC,∴![]() ,∵AH≤AN=3,AB=4,∴当点N、H重合(即AH=AN)时,AH最大,BH最小,CF最小,DF最大,此时点M、F重合,B、N、M三点共线,如图3所示:
,∵AH≤AN=3,AB=4,∴当点N、H重合(即AH=AN)时,AH最大,BH最小,CF最小,DF最大,此时点M、F重合,B、N、M三点共线,如图3所示:
由折叠性质得:AD=AH,∵AD=BC,∴AH=BC,在△ABH和△BFC中,∵∠HBA=∠BFC,∠AHB=∠BCF,AH=BC,∴△ABH≌△BFC(AAS),∴CF=BH,由勾股定理得:BH![]() =
=![]() ,∴CF=
,∴CF=![]() ,∴DF的最大值=DC﹣CF=
,∴DF的最大值=DC﹣CF=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】亚洲陆地而积约为4400万平方千米,将44000000科学记数法表示为( )
A. 4.4×107B. 4.4×106C. 0.44×107D. 4.4×103
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2012年6月2日新疆科克苏湿地进行第四次生态补水,补水约46万米3 , 46万米3用科学记数法表示为( )
A.4.6×106米3
B.4.6×105米3
C.4.6×102米3
D.4.6×10米3
查看答案和解析>>
科目:初中数学 来源: 题型:
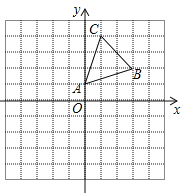
【题目】如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)将△A1B1C1沿x轴方向向左平移3个单位后得到△A2B2C2,写出顶点A2,B2,C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】环境空气质量问题已经成为人们日常生活所关心的重要问题,我国新修订的《环境空气质量标准》中增加了PM2.5检测指标,“PM2.5”是指大气中危害健康的直径小于或等于2.5微米的颗粒物,2.5微米即0.0000025米.用科学记数法表示0.0000025为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
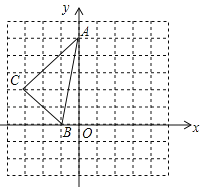
【题目】如图,方格中,每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图.
(1)画出将△ABC向右平移2个单位得到△A1B1C1;
(2)画出将△ABC绕点O顺时针方向旋转90°得到的△A2B2C2;
(3)求△A1B1C1与△A2B2C2重合部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com