
【题目】如图,一次函数![]() 的图象与抛物线
的图象与抛物线![]() 交
交![]() 轴于
轴于![]() 点,交
点,交![]() 轴于
轴于![]() 点,抛物线交
点,抛物线交![]() 轴的另一个交点为点
轴的另一个交点为点![]() (点
(点![]() 的左边).点
的左边).点![]() 为抛物线上一个动点(且点
为抛物线上一个动点(且点![]() 的横坐标
的横坐标![]() 满足
满足![]() ,过点
,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() .
.
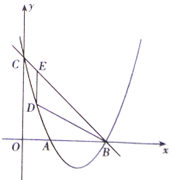
(1)求该抛物线的解析式;
(2)若![]() 为直角三角形,求点
为直角三角形,求点![]() 的坐标;
的坐标;
(3)在(2)的结论下,点![]() 为抛物线上任意一个动点,点
为抛物线上任意一个动点,点![]() 为
为![]() 轴上一个动点,则以
轴上一个动点,则以![]() ,
,![]() ,
,![]() ,
,![]() 四点为顶点的四边形能否为平行四边形,若能,请直接写出点
四点为顶点的四边形能否为平行四边形,若能,请直接写出点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
【答案】(1)y=x2﹣4x+3;(2)D点坐标为D1(1,0),D2(2,﹣1);(3)能,![]() ,
,![]()
【解析】
(1)先求出点B、C的坐标,然后利用待定系数法,即可求出抛物线的解析式;
(2)根据题意,可分为两种情况进行①当点D1为直角顶点时,点D1与点A重合;②当点B为△BD2E2的直角顶点时;分别求出坐标即可;
(3)由题意,利用平行四边形的判定和性质,通过平移直线BD进行讨论,即可求出点P的坐标.
解:(1)由一次函数![]() 的图象交x轴于B点,交y轴于C点可得,
的图象交x轴于B点,交y轴于C点可得,
∴B(3,0),C(0,3),
把B、C代入抛物线![]() 可得,
可得,
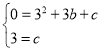 ,
,
∴![]()
∴抛物线为y=x2﹣4x+3;
(2)分两种情况:
①当点D1为直角顶点时,点D1与点A重合;
令y=0,得x2﹣4x+3=0,
解得:x1=1,x2=3;
∵点B在点A的右边,
∴A(1,0),B(3,0);
∴D1(1,0);
②当点B为△BD2E2的直角顶点时;
∵OB=OC,∠BOC=90°,
∴∠OBE2=45°;
当∠E2BD2=90°时,∠OBD2=45°,
∴BO平分∠E2BD2;
又∵D2E2∥y轴,
∴D2E2⊥BO,
∴D2、E2关于x轴对称;
直线BC的函数关系式为y=﹣x+3;
设E2(x,﹣x+3),D2(x,x2﹣4x+3),
则有:(﹣x+3)+(x2﹣4x+3)=0,
即x2﹣5x+6=0;
解得:x1=2,x2=3(舍去);
∴当x=2时,y=x2﹣4x+3=22﹣4×2+3=﹣1;
∴D2的坐标为D2(2,﹣1).
∴D点坐标为D1(1,0),D2(2,﹣1);
(3)由(2)知,当D点的坐标为D1(1,0)时,不能构成平行四边形;
当点D的坐标为D2(2,﹣1)(即抛物线顶点)时,
平移直线BD交x轴于点N,交抛物线于P;
∵D(2,﹣1),
∴可设P(x,1);
∴x2﹣4x+3=1,
解得:![]() ,
,![]() ;
;
∴符合条件的P点有两个,
即![]() ,
,![]() .
.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】疫情期间,甲、乙两个口罩工厂共同承担口罩生产任务,甲工厂单独完成此项任务比乙工厂单独完成此项任务需多用10天,且甲工厂单独生产45天和乙工厂单独生产30天的工作量相同.
(1)甲、乙两工厂单独完成此项任务需要多少天?
(2)若甲、乙两工厂共同生产了3天后,乙工厂因设备检修停止生产,由甲工厂维续生产,为了不影响任务进度,甲工厂的工作效率提高到原来的2倍,要使甲工厂总的工作量不少于乙工厂总的工作量的2倍,那么甲工厂需要至少再单独生产多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用36万元购进A、B两种商品,销售完后共获利6万元,其进价和售价如下表:
A | B | |
进价(元/件) | 1200 | 1000 |
售价(元/件) | 1380 | 1200 |
(注:获利=售价-进价)
(1) 该商场购进A、B两种商品各多少件?
(2) 商场第二次以原进价购进A、B两种商品.购进B种商品的件数不变,而购进A种商品的件数是第一次的2倍,A种商品按原价出售,而B种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于81600元,B种商品最低售价为每件多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织全校学生进行了一次“社会主义核心价值观”知识竞赛,赛后随机抽取了各年级部分学生成绩进行统计,制作如下频数分布表和频数分布直方图.请根据图表中提供的信息,解答下列问题:
分数段( | 频数 | 频率 |
| 4 | 0.1 |
| 8 |
|
|
| 0.3 |
| 10 | 0.25 |
| 6 | 0.15 |
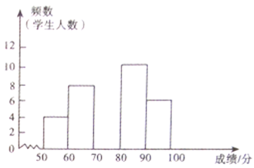
(1)请求出该校随机抽取了____学生成绩进行统计;
(2)表中![]() ____,
____,![]() ____,并补全直方图;
____,并补全直方图;
(3)若用扇形统计图描述此成绩统计分布情况,则分数段![]() 对应扇形的圆心角度数是___
对应扇形的圆心角度数是___![]() ;
;
(4)若该校共有学生8000人,请估计该校分数在![]() 的学生有多少人?
的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年全民抗疫期间,抗疫志士莫小贝购进一条生产线生产抗疫物质. 已知该生产线的三个操作平台分别排列在同一直线上,顺次是甲、乙、丙,其中甲乙平台之间的距离为40米,乙丙平台之间的距离为60米,操作甲、乙、丙平台分别需要20人、70人、60人. 由于时间仓促无法做到完全自动化,需要在三个平台之间建立一个原材料供给站让工人自取,有如下两个方案:方案一:让所有工人到供给站的距离总和最小;方案二:让甲、丙平台所有工人到供给站的距离之和等于乙平台所有工人到供给站的距离之和.
(1)若按照方案一建站,供给站距离甲平台多少米?
(2)若按照方案二建站,供给站距离甲平台多少米?
(3)在(2)的条件下,若甲平台的工人数增加![]() 人(
人(![]() ),那么随着
),那么随着![]() 的增大,供给站将距离甲平台将越来越远,还是越来越近?请说明理由.
的增大,供给站将距离甲平台将越来越远,还是越来越近?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
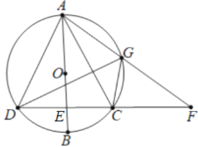
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E ,G是弧AC上的点,AG,DC延长线交于点F.
(1)求证:∠FGC=∠AGD.
(2)若BE=2,CD=8,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
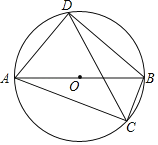
【题目】如图,AB是⊙O的直径,AC、BC是⊙O的弦,∠ACB的平分线交⊙O于D,连接AD、BD,已知AB=6,BC=2.
(1)求AD的长度和四边形ACBD的面积;
(2)证明:2AD2=AC2+BC2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (
(![]() )交直线
)交直线![]() :
:![]() 于点
于点![]() ,点
,点![]() 两点,且过点
两点,且过点![]() ,连接
,连接![]() ,
,![]() .
.
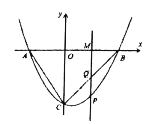
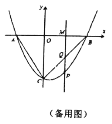
(1)求此抛物线的表达式与顶点坐标;
(2)点![]() 是第四象限内抛物线上的一个动点,过点
是第四象限内抛物线上的一个动点,过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() ,
,![]() 交
交![]() 于点
于点![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() ,试探究点
,试探究点![]() 在运动过程中,是否存在这样的点
在运动过程中,是否存在这样的点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() 为顶点的三角形是等腰三角形.若存在,请求出此时点
为顶点的三角形是等腰三角形.若存在,请求出此时点![]() 的坐标,若不存在,请说明理由;
的坐标,若不存在,请说明理由;
(3)若点![]() 在
在![]() 轴上,点
轴上,点![]() 在抛物线上,是否存在以点
在抛物线上,是否存在以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的平行四边形?若存在,求点
为顶点的平行四边形?若存在,求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com